Early British gas turbine development

[PMN1]

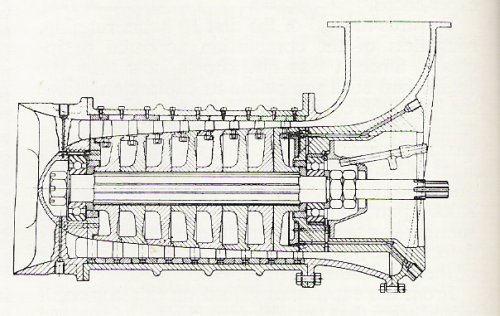
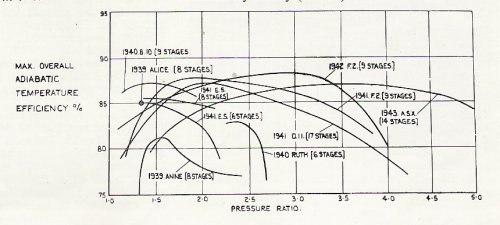
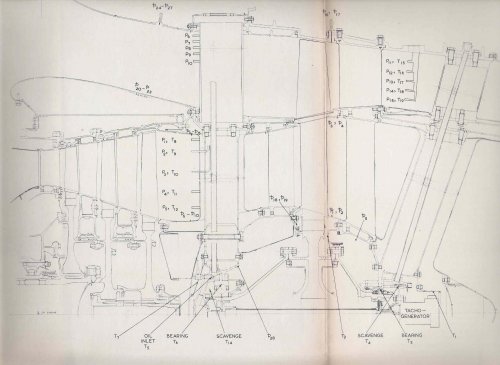
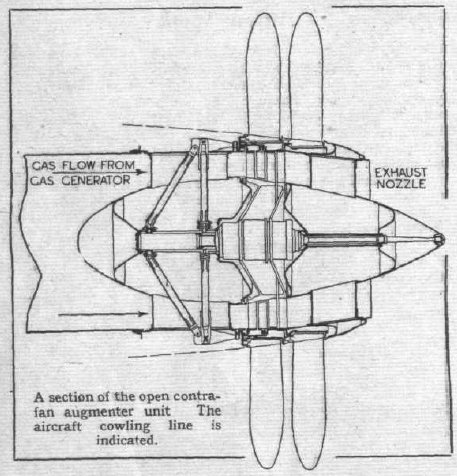
Got this form Groggy on the TGP site

http://www.tgplanes.com/Public/snitz/topic.asp?TOPIC_ID=1268

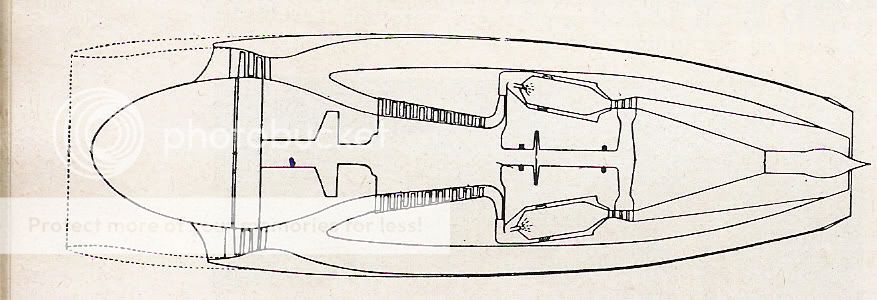
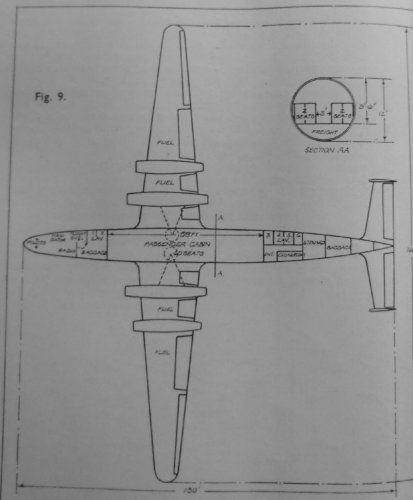
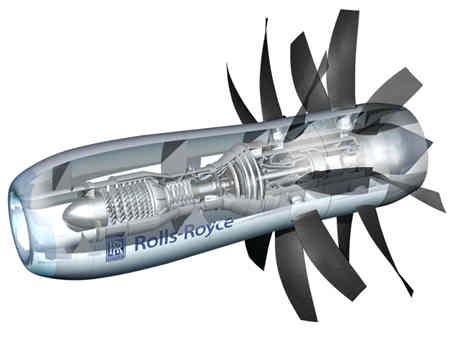
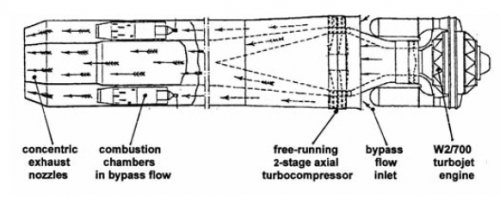
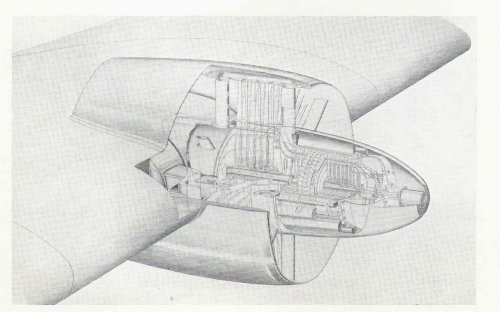
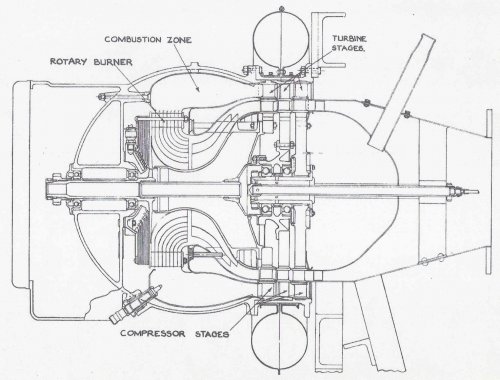
“The L.R.1 bomber project was first submitted to the Ministry of Aircraft Production late in 1944” and “In May, 1945 a project was prepared for a transatlantic civil transport powered by four L.R. 1 engines driving ducted fans. The machine was designed to cruise at 470 m.p.h. at 45,000ft. with a still air range of 5,280 miles and a payload of 20,000 lb. The estimated all-up weight was 156,000 lb.”

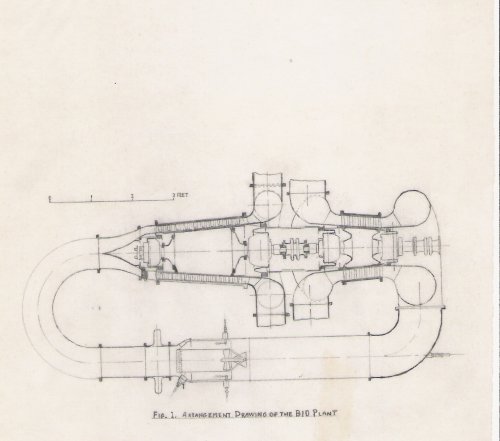
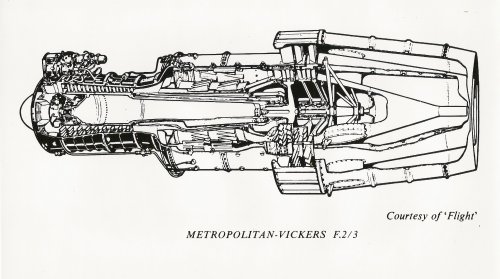
“The static thrust of the straight jet version of the engine was envisaged as 5,500lb static thrust at S.L.” The L.R.1 turbo fan would have given with a bypass ratio of 2.5, so this would give a thrust of ?? 10,000 lb? any ideas?

This is about the only details I can find for the L.R. 1 bomber but I was told by Ian Whittle, Whittles son that the prototype L.R.1 engine was almost finished being built.

Any additions or comments?


Anybody have any further information on the bomber, the civilain transport or the engines and what would have been the effect on the early post war designs if a turbofan had been available in the late 40's

 

[Spark]

Frank Whittle's axial jet, turbofan.
After Frank Whittle left Powerjets worked on continued on his axial turbofan and turbo prop.
It was finally tested circa 1947. But worked stopped with the failure of the gearbox. Can any one help with photos, details , drawings?
Has any one anything on his axial turbofan with afterburner, reheat designed for supersonic flight

 

[Apophenia]

Spark, are you referring to the Power Jets L.R.1 axial-flow engine? If so, this entry in Cambridge's Janus site may be a lead:

http://janus.lib.cam.ac.uk/db/node.xsp?id=EAD%2FGBR%2F0014%2FWHTL%20AS%202

Whittle Associated Papers

Power Jets (Research and Development) Ltd Projects Department Note No. A.137 (a). "Power Jets L.R.1 Engine". With diagrams and designs. 29 January 1945

 

[red admiral]

Genesis of the Jet, by Golley and Gunston has some details in the appendices of Whittle's work with thrust augmentors, turbofans and reheat. There are diagrams, but no photos.

I've never heard that the engines were ever finished or tested. From reading other accounts it seems that PowerJets didn't do any further work on whole engines after being nationalised in 1944, just research into bits. Engine development was given by MAP to the aircraft companies.

 

[alertken]

The Royal Aircraft Factory lost its role as designer of complete vehicles in 1918 and became the Basic, or Pure Research resource. Govts. took the view that the State, in academia or Establishments, should create the knowledge that industry should Apply. RAE organised into specialities, inc. Powerplant. So it was; then Whittle came up with gyre-power just as "Hyper" reciprocating engines were being explored. 1938-41 A.M/MAP perceived that ASM, Bristol, Napier and RR had their hands full making mere Cheetah, Hercules, Dagger, Merlin work, while trying to invent Deerhound, Centaurus, Sabre, Griffon. It would be nugatory to put a wholly new technology there, when logic was to find metalworkers familiar with discs, spin. So, superchargers: GE's 25% affiliate AEI (BTH & Metro-Vick). (Parallel in US - NACA; Pratt/Wright overloaded on big pistons, so enter Allis Chalmers, GE, Westinghouse). Fabrication capacity was idle in the auto industry, so enter Rover, Vauxhall (US: Buick, Studebaker). Geo.DH had some of F.Halford's time, and had capacity beyond Gypsies, and Merlin repair, so was given access to Whittle's work, to evolve Goblin.

As 1942 became 1943, big pistons were fixed and in production, even Service. Massive investment was churning out aero-engines from the original Ring of 4, plus shadows. Stafford Cripps had been the Counsel who had extracted damages from Rootes for infringing Ricardo's diesel compression swirl chamber. Appointed MAP Nov.,1942, despite having been in 1938 so Left Wing that Attlee had expelled him from the Labour Party, he chose to reject Whittle's advice that the entire aero-engine industry should be nationalised (A.Nahum,F.W - Invention of the Jet,Icon,2004,P.105). Instead he: introduced Board harmony at Bristol by taking Fedden as his Special Technical Advisor (Nov.1942); fixed Napier's management shortcomings by causing EE to buy them (Dec.1942); took Rover out and put RR in to W.2-fabrication; buying Power Jets (March,1943) and turning it, at Harry Ricardo's suggestion (Nahum,P.100), into RAE's gyre lab (to be the National Gas Turbine Establishment). So, no change then: Basic Research: NGTE; Applied Research, product development and supply: industry. Same as most munitions bar the actual bangs; same as US.

Why people continue to bang on about maltreatment of Whittle is baffling (not talking about £100K for his invention; but about non-expansion of his lab into a factory). Why would any Minister render idle the engineering competence of an industry dating back to 1909, by duplicating it in an incomer? The reason for parking many of Whittle's schemes in 1944 was neither personal jealousy, not any conspiracy, but simple need: we had no need for plenum chamber burning, or long range turbofans. The War would be resolved on products in prototype by 1942. The Days after VJ Day were for converting swords to ploughshares. From 1947-50 we tried to make colder, easier axials work. Korean War money caused us to do Conway (which stemmed from L.R.1, via Napier E.113), Gyron; both, plus PCB work at BSEL from 1960 (to be BS.100) drew upon NGTE Basic Research which derived from Whittle-memory. A key NGTE scientist in BS.100, Ray Holl, had been in Power Jets. Whittle's legacy is no less secure than if his advice had led to one UK Gyre Co with he as President-Emeritus.

 

[Spark]

[/quote]

Hi
will make a proper reply

but,
The other day I was told that some new documents had been recieved showing that in 1937 Metrovik were told or had started by themselves looking at an idea for a jet engine? Will check this story again next week:

This rather early and is against the generally exceptd wisdom?

 

[red admiral]

A visit was made by the RAE to Metropolitan Vickers on 3rd June 1937 and three designs outlined.

I'll write up a bit more of the information I have later.

 

[red admiral]

Sorry for the delay;

The Early History of the Aircraft Gas Turbine in Britain by W Hawthorne

 

[tartle]

If memory serves me right
....the RAE were pioneers of axial compressors... The 'Betty' is a Haynes Constant Research rig building on the axial compressor work of A A Griffith and after several rig designs eventually led to the Metrovick engines such as Beryl... this series of engines led to the Sapphire, production of which was handed to Armstrong Siddeley, plus further development. Metrovick an American owned company set up at the turn of the century had a long relationship with RAE, no doubt due to their rotating machinary expertise (electricity!). They helped with supercharger design for RAFactory in WW1.
See also this post I have written elsewhere on secretprojects.

 

[tartle]

In case people are still interested ...
the Whittle engine looked like this...........

There were various versions proposed based on this layout..
The one in the diagram is a 2.5:1 bypass ratio single-shaft - 8-stage axial plus 1 stage centrifugal driven by a 2-stage turbine; the turbofan is geared off the front of the compressor turning at 2,300 rpm; the engine itself at take-off rotates at 8,000 rpm. This turbofan is based upon the original six-blade contra rotating turboprop version which was projected to supply 4,870 shp plus 3,160 lbt at take-off.
The 'fan version was designed to give 2,800 thp at cruise with a fuel consumption of 1,890 lb/hr at a weight of 2,770lb.
Leaving off everything forward of the compressor gave a jet of 2,600 lb weight and a static sea level t/o thrust of 5,500 lb.
Yet another version had a separate turbine driving a ducted fan; a further variant was to have the turbine drive a propeller proposed for a 300 mph cruise at 20,000ft aeroplane project that eventually became the Britannia.
The LR1 project was serioius enough for the MAP powerplants committee to order one prototype engine plus spares in Aug 1945. The compressor was run at Pyestock and in 1949 a mechanical failure occured and the project was abandoned. So I am not sure if there ever was a complete engine... maybe NGTE, Pyestock archives hold the answer?

 

[red admiral]

Interesting information tartle. I seem to remember from Gensis of the Jet that Powerjets were constructing a complete engine in 1944/45 -ish with construction proceding to an advanced stage. I've no idea what archives remain at Pyestock; they might have been subsumed into FAST in Farnborough at some stage?

 

[tartle]

red admiral,
I'll do some checking. FAST is a good lead.

 

[Jemiba]

From The Aeroplane, March 1959, a design for a transatlantic civil transport, powered
by four L.R.1 engines. With an all-up weight of 156.000 lbs (70.760 kg), the aircraft was
expected to cruise at 470 mph (756 km/h) at a height of 45.000 ft (13.700 m)with a range
of 5.280 miles (8.500 km) and a payload of 20.000 lbs (9.070 kg) .

 

[Stargazer]

http://www.tgplanes.com/Public/snitz/topic.asp?TOPIC_ID=1268

Just two concerns:
1°) You need to be logged (therefore a member) of said site to be able to view the page you linked.
2°) You do not specify what aircraft manufacturer originated the L.R.1 bomber project. Was that Gloster, given the Whittle connection?

 

[alertken]

I think jemiba's #4 is an aero-engine man's concept, not an airframer's scheme.

My understanding of UK's evolution of augmented flow:
1944: Power Jets had as rig hardware, W.2/700, which we would now label as a PCB turbofan. As a components exercise PJ had LR.1. Whittle was pressing Minister Cripps to nationalise the entire aero-engine industry, and generally was being "difficult". 28/4/44 Cripps nationalised Power Jets.

1/7/46 it subsumed RAE's powerplant resources, becoming NGTE. Basic Research: Establishment, Applied Research: industry, same as airframes. Augmented flow passed to Napier, schemed as E.132.
1946: UK was trying hard to make axial turbojets work, without notable success. English Electric's entry to modern aero design hinged on A1, whose AJ65 was dammed.

July,1947: EE's Medium Bomber bid, and Short's enhancement of Sperrin, both based on E.132, both rejected by MoS.
EE's Geo.Nelson (owner of Napier) sold E.132 to RR. Hives parked it with his Chief Scientist, AA Griffith, while practical folk tried to make Avon as good as ASM's Sapphire, just acquired ex-MetroVick F.9.

1949: Avon improves and sells. Griffith is sponsored to start on (E.132, enhanced as) RB80, chosen:

1950: as Conway for Valiant B.2, 17 ordered 10/51, cancelled. Conway continued for V.1000, cancelled. RR took a fixed production price punt to displace Olympus 201 from Victor B.2, then found berths in 707-420/DC-8/40.

Points: A) what if...augmented flow had flowed smoothly through 1947-54. Well, why would it do so, when Avon et al did not?
B ) just to keep perspective on the who-though-of-it-first game: GE axial J35/J47 combustor “drew on Whittle” and was derived from W.2/700, which used GE compressor rotor; this, the first by-pass turbofan, influenced RB80 Conway, which eroded 1960s’ sales of GE first attempt on the civil market - CJ-805-23. Gunston,Engines,Pp61/108.

 

[tartle]

The original gas turbine aerodynamic work undertaken by Whittle was, I always understood, based on the use of a centrifugal compressor using Ellor's supercharger aerodynamic work together with an axial turbine based on the 'aerodynamics' of steam turbines. His genius was stitching it all together and developing combustion chambers or cans that could burn the fuel in a contained way to generate the energy to drive the turbine and give exhaust thrust. At RAE Griffith's genius was to recognise that upto 1926 axial compressor design theory meant all practical designs to date were running with stalled blading. Hayne Constant worked alongside Griffith and continued the work after G left for RR. They originally carried out extensive cascade work to prove out their theoretical methods and then in 1937 commissioned the construction of a test compressor ' a' nicknamed Anne. Work had been proceeding on a distributed gas turbine and it was decided to build one to be called B10 or Betty. Whereas Anne had been built by Allis Chalmers, Betty was made by Metropolitan Vickers with the input of their steam turbine engineer David Smith. Betty was run in Manchester at Metrovick's Trafford Park complex. The Museum of Science and Industry has artefacts on display that are relevant so I dashed into the Hall and took some photos... the place relies a great deal on natural light and it was near dusk and I used my 'phone to get shots.. hence quality! The cascade and Anne are not there so I have used copy of pics from my archive...
mpre on RAE work in Flight report of Hayne Constant's Sir Henry Royce Memorial lecture in 1957
Betty is there and there are shots below. Also a layout diagram I traced in the 1960's . You can see the volute and 4 stage turbine on the layout. RAE realised distributed machinary was not the answer and schemed a more conventional layout... F.1 which was passed to David Smith... his team produced the F.2/1 followed by F.2/2. Whittle's turbofan or augmentor concept based on RAE work was also incorporated as the F.3 augmentor.

 

[tartle]

The B10 Betty layout drawing above can be read with the diagram in an earlier post ...
The flight engine F2/1 is shaown.. it went in the tail of a Lancaster.
The F.2/2 engine is also at MOSI, which can, and was combined with the F.3 Augmentor. Pictures below.
...and a Flight cutaway of the whole rear fan engine. There is another view of this cutaway with the addition of a sectional view and the aerofoil cross-sections on the Flight website.

 

[Johnbr]

Thanks you made my week.

 

[tartle]

.... and a x-section of Anne from my archive: 6 inches in diameter over the blades.

 

[tartle]

I have been waiting for this book to be published... it arrived yesterday and I realised even more how much we owe to A. A. Griffiths's early work in rotating machinery.......
David Bloor's new book "The Enigma of the Aerofoil: Rival Theories in Aerodynamics, 1909-1930" tells the story of two theories intended to explain the origin and nature of the lift of a wing. They may be called the Discontinuity Theory and the Circulatory (or vortex) Theory. Eventually the latter (Gottingen) theory became the accepted one and the other (Cambridge) one fell by the wayside.
The book written after researching the Archives of the relevant people and institutions is a fascinating account of how they theories did or did not develop and how difficult it was for the British 'camp' to get on board the Gottingen Theory 'boat'. Bloor's conclusion is quite complex and he emphasises his simple one can be taken too literally i.e. Because the British placed aerodynamics in the hands of mathematical physicists while the Germans place it in the hands of mathematically sophisticated engineers!
Fortunately Griffiths, whilst mathematically accomplished went, not to Cambridge but to Liverpool where he obtained his B.Eng(1914), M.Eng(1917), and D.Eng(1921) from Liverpool University’s School of Mechanical Engineering; he was to make effective use of the theory.

 

[tartle]

In July 1926 A. A. Griffiths wrote a seminal paper (RAE report H.1111- An Aerodynamic Theory of Turbine Design) in which he demonstrated that the axial gas turbine was feasible as a power unit for aircraft propulsion and determined the basis for a complete design. He wrote:
“The comparatively low efficiency of turbines and turbo-compressors is the only serious obstacle to the development of a successful internal combustion turbine suitable for use on aircraft. The causes of this low efficiency have been investigated.
The circulation theory of aerodynamics has been applied to the problem of the design of turbine blading. It has been deduced that the main reason for the low efficiency of blades of current design is that they normally work under stalled conditions. Formulae for efficiency have been worked out on the basis of the new theory…..
It appeared on consideration that the use of rotary members similar to airscrews would lead to much higher efficiencies than are at present obtainable from turbo-machines. With existing airscrews, propeller efficiencies as high as 0.80 to 0.85 can be readily obtained. By using airscrews as the rotary members of compressors, even higher efficiencies would be possible since most of the translational energy in the slipstream would be recoverable in the stator blades. Moreover the efficiency of the airscrews can be predicted within narrow limits by the application of known aerodynamic principles, so that the conditions for maximum efficiency are comparatively easy to determine.
These considerations at once suggest the new method for designing turbo-machinery. The blades, instead of being regarded as the walls of channels, whose shape determines the velocity and pressure changes taking place in the fluid, are to be regarded as aerofoils and the changes in velocity and pressure are to be calculated from the blade reactions. These, in turn, can be found with the help of the known aerodynamic characteristics of the blade sections……
A point which emerges at once is that, since the angle through which the fluid stream can be efficiently turned by one row of blades is comparatively small, it will usually be necessary to use multi-stage designs in order to secure a high overall efficiency.”
The A. R. C. discussed the paper and recommended experiments on a single-stage compressor and a single-stage turbine; this was constructed in 1927 under Griffith’s supervision.
The small test unit comprised a compressor and turbine mounted on one shaft and having blading of aerofoil section. The diameter of the rotor barrel was 3 in. and the internal diameter of the casing 4 in. giving a blade height of 0.5 in. less blade tip clearance; the blade section had a chord of 0.6 in.
A. C. Clothier’s tests showed that the unit gave efficiencies that tied in well with Griffith’s prediction and reached 91% including blade, casing and rotor friction losses and windage on rotor ends but neglecting bearing friction losses, at speeds around 15,000 rev/min. This was the first time that high efficiency was obtained from an axial type compressor; Griffith may be said to be the true originator of the multi-stage axial engine.
[Most of the above comes from the Royal Society's Biographical Memoir on A. A. Griffith.]
The effect of the new theory on efficiency can be seen in the graph plotting RAE turbomachinery and their derivatives.

 

[tartle]

In 2008 the F.2/1 was in a better position for photography.

 

[red admiral]

Thanks for the pictures and information there. I think I've got a couple of papers on Griffith's gas turbine work which might be worth summarising here.

Pictures attached are from the complete F3 engine at RRHT Derby, unfortunately not very good quality.

 

[tartle]

My reaction is RR Derby... could this be the Aft fan Avon? I'll examine pics with a close scrute later and look at my Aftfan Avon stuff

 

[red admiral]

My reaction is RR Derby... could this be the Aft fan Avon? I'll examine pics with a close scrute later and look at my Aftfan Avon stuff

It's another Metrovick F3 at Rolls-Royce Heritage Trust Derby. Not an Avon due to the lack of can-annular combustors (and I seem to remember a Metrovick plaque/board next to it).

The article I mentioned previously is "Alan Arnold Griffith. 1893-1963" by "AA Rubbra" published in Biographical Memoirs of Fellows of the Royal Society, Vol. 10 (Nov., 1964), pp. 117-136

 

[tartle]

I have quoted from Rubbra's article in #20 above.
The Avon started with individual combustion cans but swapped to a can-annular design from the RA.14 onwards. There are RA.1 and RA.28 photos below to illustrate the changes. The RA.14 onwards incorporated lesson learned from the Sapphire compressor data released to RR at the request of the MoS.
The RA29 or 300 series had a zero stage on the compressor and a third turbine stage added... the Aft Fan version was intended to be behind one of these engines.
The Aft fan version of the Avon is listed in the catalogue but I have asked Derby to tell me what it is.

 

[tartle]

Here is a section of the aft fan Avon ... the fan blade has a diameter 50 in. The close integration with the RA.29 can be seen; note the three turbine stages on the Avon itself. built as a response to the General Electric CJ805-23 aft fan fitted in a Caravelle..neither engine manufacturer attracted an order... the Avon went on to be used for noise research supporting the RB.211 programme. The Convair 990 was fitted with the GE aft fan .. a front and rear view of installed CJ805-23 are below.

 

[tartle]

Having consulted Mike Evans, who set up the Rolls-Royce Heritage Trust I can confirm that there is a Metrovick at Derby. It is an F.2 turbojet. He confirmed the pictures in #22 are in fact of the Avon Aft Fan. I thought the intake was familiar, see #26, from my time at Hucknall in the '60s when it was on noise, etc. test there.
There was another aft fan version built by Metrovick and this was an open prop concept. Flight describes it here
Yet again it shows ideas based on 'science' can come around again as the external constraints to adoption change and the technologies at 'the fingertips' changes the economics... it is well worth revisiting to see if an idea has become one with legs. Rolls-Royce are at present in a research programme being driven by the desire for cleaner engines. They are involved in Sustainable and Green Engine (SAGE) Integrated Technology Demonstrator Programme described here.
and here.
This is an extract of the RR description:
"Open rotor technologies offer the potential for significant reductions in fuel burn and CO2 emissions relative to turbofan engines of equivalent thrust. Higher propulsive efficiencies are achieved for turbofans by increasing the bypass ratio through increases in fan diameter but there is a diminishing return to this improvement as nacelle diameters and consequently weight and drag increase. Open rotor engines remove this limitation by operating the propeller blades without a surrounding nacelle, thus enabling ultrahigh bypass ratios to be achieved.
Further improvements in propulsive efficiency can be gained for open rotor engines by using a second row of propeller blades rotating in opposition to the front row to remove the spin from the column of air to give a more direct thrust. "
Which feels like a rewrite of AA Griffith's report, #20, above

 

[tartle]

In #20 above we read that Griffiths was predicting that compressor stage efficiencies of 90+% should be achievable and that tests corroborated it. This left me curious ... I listen to Radio 4 guerilla economist Tim Harford and the More or Less team investigate numbers in the news... "double the risk of" headlines that cause concern but actually mean going from 1 in a million to 2 in a million... we needn't worry after all.
So what is the context of Griffiths' statement .... does it mean going from 88 to 91 or what?
Not quite as easy to find the answer as I hoped but when I did it is obvious why people sat up and took notice.Charles Parsons who was our great Victorian/Edwardian pioneer of steam turbines for industrial and marine use (e.g. Turbinia) decided to use steam turbine blading in reverse and built an axial compressor.. it had less than 40% efficiency but he perservered because of other advantages over the reciprocating compressors that were used in mines and steelworks at the time. That is lack of pulsation, size, weight, and less maintenance. He managed to get the efficiency up to 55% and in the early years of the 20th century delivered 17 machines mainly for blast furnace use... then Rateau came along with multi stage centrifugal designs of 70% efficiency and the market for axials disappeared. So when in 1926 Griffith realised why the axial had such a low efficiency and had design methods to raise it 20% above the centrifugal people began to take the axials seriously again. At this stage work on industrial and aero applications diverged and did not come together again until Avons and Olympus were used in industrial/marine applications afte WW2.
Picture from 'Galaxies and Machines' book on Parsons.

 

[tartle]

The'Aeronautical Journal' March 2010 included a paper 'On the Aerodynamics of the Miles M.52 (E.24/43) - a historical perspective.
It included a Power Jets sketch of the M.52 engine: a W2/700 with a No. 4Design Thrust Augmentor and afterburner, a photo of the 2-stage aftfan augmentor wheels and a further photo of the assembled engine to be tested.
Also an excerpt describing installation and the relevant conclusions. Picture titles also include the source reference.

 

[taildragger]

This is an extract of the RR description:
"Open rotor technologies offer the potential for significant reductions in fuel burn and CO2 emissions relative to turbofan engines of equivalent thrust. Higher propulsive efficiencies are achieved for turbofans by increasing the bypass ratio through increases in fan diameter but there is a diminishing return to this improvement as nacelle diameters and consequently weight and drag increase. Open rotor engines remove this limitation by operating the propeller blades without a surrounding nacelle, thus enabling ultrahigh bypass ratios to be achieved.
Further improvements in propulsive efficiency can be gained for open rotor engines by using a second row of propeller blades rotating in opposition to the front row to remove the spin from the column of air to give a more direct thrust. "
Which feels like a rewrite of AA Griffith's report, #20, above

From the dumb questions department:
Is there any clear technical distinction between "open rotor/UDF" and "turboprop"? What I've understood to be the defining characteristics of the UDF/open rotor (blades coaxial with turbine, scimitar shaped blades, pusher configuration) have all been applied to earlier engines that were known as turboprops. If it's just marketing, maybe a less technical-sounding label is the answer - how about "DreamPusher", or has Boeing already trademarked that?

 

[JFC Fuller]

At this stage work on industrial and aero applications diverged and did not come together again until Avons and Olympus were used in industrial/marine applications afte WW2.

On that subject, a range of innovative things were done with Gas Turbines post war for the Royal Navy, including with the Metrovick designs which were actually used on a number of ships. The Metrovick G2 for instance was used in the Bold class fast attack craft whilst Grey Goose was refitted with two RR units going by the designation RM60 which were intercooled and recuperated. The RM60 was first ordered by the Admiralty in 1946 though it did not go to Sea until 1953. Apparently the USN ordered two (also a pair of G2s) though they seem to have never been delivered as only three were made of which two were fitted in Grey Goose.

 

[tartle]

I should have mentioned Metrovick's marine work...
On the subject of naming I remember Ric Parker, technology chief at RR (what a job!) telling us at a Judge Institute presentation that

"In recent years, the drive for more efficient and quieter turbofans — the engines that power most civil airliners — has seen the introduction of ever-larger fans in an effort to route a larger mass of air around the turbine than passes though it. These engines are said to have a higher bypass ratio.

However, there are limitations to the gains possible with existing designs. As you come up and up in fan diameter, you get to a point where the weight of the fan and the drag from the casings start to eat into that efficiency. ’The idea was to go back to propellers, get rid of the fan case, get rid of all this extra weight around it and then you can make your blades 4m in diameter.

Although the open-rotor concept bears a passing resemblance to the traditional propeller, there are considerable differences. Conventional props limit the speed of the aircraft. The big difference between the open rotor and the prop is that there will be two rotors spinning in opposite directions. In a conventional prop, the air itself comes out spinning so only part of the momentum is pushing the aircraft forward; the rest is trying to turn itself around and is wasted. If you put a second rotor spinning in the opposite direction, you can speed up the air, but you also take out the spin, so you finish up with a high-speed propeller that can propel the aircraft at the sort of velocities and altitudes they fly at today but with probably a 15 per cent better fuel efficiency than an enclosed fan."

This is a subtle but crucial difference in the duty of the propulsion device. As a simple engineer I like to think of the design effort needed to design the component .. In a compressor blade the untwisting effect due to centrifugal force on each blade section is small and can usually be ignored. But for a fan blade this cannot be ignored. In the older design of clappered blade the clappers had a clearance and the rattling of the blades as the engine turned over in the wind could be heard as we went up the stairs into the cabin... however when the engine was running in the air the centrifugal twist would lock up the clappers so much that the faces had to be hard coated with stellite to prevent wear.
So with a propeller the aerofoil sections are virtually placed on a radial line through their centres of area (simplistic, I know). With a propfan the revs are higher and the tip sections are running at M0.8 or so ... think aircraft wings at this speed .. they tend to be swept.. so the sections of the propeller are arranged to sweep the leading and trailing edges relative to the incident streamlines... so the forces generated will tend to distort the prop... so we need to design for the running aero-structural condidtions hence the technology is a step or two from how we design conventional propellers.. hence the name change to acknowledge this when talking to non-technical people who hold the purse strings.... at least that is how I interpret it!​

Here is a picture of me using the best technology available at the time to design a fan blade.. rumour has it that they scaled down the RB.207 so the blade fitted my drawing board (on the right).​

 

[Spark]

Hi tartle.
There was, is a Metrovik marine turbine at the Science Museum London.

I should have mentioned Metrovick's marine work...

 

[tartle]

You sparked a memory......In 1947 a Metrovick G.1 Gatric gas turbine was fitted to the MGB 2009, making it the world's first gas turbine powered naval vessel. The Gatric was based on the F.2 engine with a free power turbine in the exhaust outlet and was modified to run on diesel fuel.
The shipping? gallery was refurbished a couple of years ago and includes the Metrovick propulsion unit.
The curator took this photo.
There are some details of the Metrovick and the RM60 here.


From Nature 20 September 1947.
50 YEARS AGO
‘Gas-Turbine Propulsion in a Naval
Vessel’ — Messrs. Metropolitan-Vickers
Electrical Co., Ltd., Trafford Park,
Manchester, have installed gas-turbine
propulsion equipment in the
experimental naval craft, M.G.B. 2009,
the trials of which will take place in the
near future. The Company claims that
this is the first naval vessel ever to be
propelled by a gas-turbine. The
characteristics of the simple-cycle gasturbine
include low overall specific
weight and size with rapid starting, and
these qualities make it very suitable for
light vessels where high speeds may
be required for limited periods and at
short notice. In M.G.B. 2009, normal
cruising and astern power is provided by
two 1,250 B.H.P. 2,400 r.p.m. Packard
internal combustion reciprocating
engines, each engine driving its own
propeller through a reduction gear.
Maximum ahead power is obtained by
bringing into operation a completely
independent Metropolitan-Vickers gasturbine
of 2,500 B.H.P., which drives a
third propeller through speed-reduction
gearing to supplement the power of the
reciprocating engines.

2nd picture from Science and Society Picture Library

 

[red admiral]

Thanks very much for your efforts here tartle. There's a lot of information to digest. I'll have to have a good read through and see what memories it kicks off.

 

[tartle]

red admiral... glad you like it.... a pleasure to share!
In the mean economic times we are in it is useful to remember our engineering heritage and the fact it relied on great people... at all levels. I have tis photo in my archives that should be a fitting tribute to what we are discussing here... teamwork that produces major innovative products that 'changes our world'.The two 'leaders' in the photo are David Smith who was key in getting the aero- and structural- dynamics right, and Robert Whyte, superintendent of the Gas Turbine Department, who got the manufacturing quality required to deliver David's vision. I salute them!

Left to right: Bill Node Ralf Cooke – Assistant Superintendent of Barton Works Robert R. Whyte SAAF representative Bill Smith – Foreman Fitter Eric Strong Chief Production Engineer Dr. David M. Smith FRS – Chief Engineer RCAF engineer Dr. J. S. Shannon – Assistant Chief Engineer SAAF engineer Bert Hall – Foreman RCAF engineer

 

[tartle]

A better picture of the MOSI aft fan... courtesy and copyright of Silicon Owl

 

[tartle]

Whittle was one of the earliest protaganists for the turbofan engine... however early in the development of the Whittle engine concepts the added complexity outweighed any calculated advantage so it was not picked up again until around WW2. Griffiths certainly thought about turboprop engines early in his axial gas turbine thinking but also reverted to a simple jet concept especially as his quest for aerodynamic efficiency drove him towards contra rotating stages that eliminated the static stator stages. These concepts were worked on well into the second world war after he moved to RR.........
Design work on Rolls-Royce’s first gas turbine engine started in September 1940. This was the CR.1, shown in the first illustration below. The large blades at the rear are an application of the engine in a ducted fan application. This part of the engine was never made. The front, smaller part is the engine itself and consists of 14 rotors freely rotating on a fixed central shaft. Each disc moves in the opposite direction to its neighbours. The inner section of the blades are compressors. Air travels from the inlet ducts to the rear of the engine and thence forwards through the compressor to the rotating burner where it is expanded very gently as it travels rearwards through the 14 turbines which make up the outer rows of blades. The high pressure ends coincide, reducing leakage from the compressors to turbines to a minimum. Also the compressor air had some cooling effect on the turbine blade roots.
The engine was first tested in 1942 and it did give 350 lbs of thrust. This design was overtaken by Whittle’s classic work and so the Griffith concept was abandoned. [description above was delivered in a lecture by J. D. Pearson in 1955]
The combustion chamber (line diagram of the rig to test this below) was of a rotating burner design. The diffuser section leads to a spherical combustion chamber housing a rotating burner dividing the chamber into eight sections. The fuel inlet is at the front of the chamber and feeds fuel into a fuel sprayer which, due to its rotation, flings the fuel into the combustion chamber proper which leads the hot gases rearwards into the "nozzle guide vanes". The rotating burner is connected to the first stage turbine wheel.
The chamber, in fact, never worked and the engine itself was equipped with 4 Welland combustion chambers.
The turbine outlet is a peripheral outlet formed as the gas flow is turned through 90 degrees.
The engine itself was 71.66" long and had a diameter of 37". Max power was 365 lb. at 5,800 rpm. giving an sfc 1.25 lb/lbt/hr.
Compression ratio was 3.05 and air mass flow was 11.1 lb/sec.
The first rotors had 46 blades per stage, later ones were tried with 60 blades.
In the 1960s the engine was one of the exhibits in the Propulsion Department, at the College of Aeronautics, Cranfield.....
Part or all of the engine is now at the Derby RRHT.

 

[Johnbr]

Thanks for the great find