SCS sub-orbital two-stage spaceplane

[hesham]

Hi,

the Vela Technology Development design the SCS (Space Cruiser System),
it is reusable piloted passenger carrying sub-orbiter two-stage spaceplane.

 

[FutureSpaceTourist]

I believe Vela shut-up shop in 2006. Certainly their website spacetrans.com disappeared in the 2nd half of 2006 and I found nothing more recent elsewhere with a quick web search.

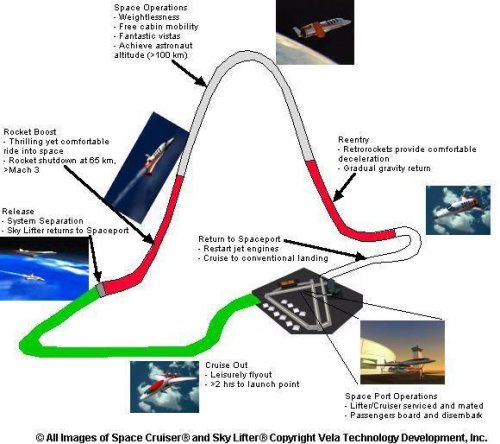
However, their two-stage suborbital system - Sky Lifter carrier aircraft and Space Cruiser spaceplane - is interesting as it has a number of similiarities with WhiteKnightTwo and SpaceShipTwo whilst being designed/in initial development in the late 90s prior to SpaceShipOne. One feature of note is that despite being a two-stage suborbital system, the spaceplane has both jet and rocket engines.

Following details (and pictures) are taken from an archived copy of the defunct website. Does anyone have any more info, particularly on how this started?

Sky Lifter

Description: Low-wing load, delta wing, twin tail, first stage, carrier vehicle.
Propulsion: Twin, pylon mounted, JT8D/F100-class turbo-jet engines, thrust 11-18k lb. each.
Crew: Pilot, Co-pilot.
Length: Estimated at 108 ft.
Wing Span: Estimated at 93 ft.
Empty Weight: Estimated at 20-25,000 lb.
GTOW: Estimated at 30-35,000 lb.

Space Cruiser

Description: Medium wing load, double delta wing, twin winglet-tails, second stage, spaceplane vehicle. During initial ascent, the cruiser is carried aloft under the lifter on a pylon.
Propulsion: 3 Nitrous Oxide/Propane, pressure fed, rocket engines (estimated thrust at 20,000 lb. each); and twin, pylon mounted, JT15D-class turbo-jet engines (estimated thrust at 2.2-4000 lb. each)
Power: Onboard jet engine and/or lifter provided (during captive carry); stored energy, probably battery (during boost, free-fall, retro); ram air turbine (during recovery), onboard jet engine (return to airport)
Crew: Pilot, co-pilot
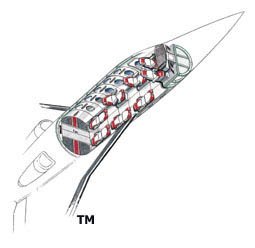
Passengers: Six (6)
Length: Estimated at 61 ft.
Wing Span: Estimated at 38 ft.
Cabin Size: Estimated at 99 in. (inner diameter), 110 in. (outer diameter), 18 ft. length
Empty Weight: Estimated at 15-20,000 lb.
GTOW: Estimated at 25-30,000 lb.

Archived copy of the flight profile is at http://web.archive.org/web/20050825213241/spacetrans.com/html/flight_profile.htm

 

[FutureSpaceTourist]

Since the above posts the following animation has been posted on youtube:

http://www.youtube.com/watch?v=GVjx-hDZIjo

 

[FutureSpaceTourist]

Found a couple more pictures from an archived copy of www.odysseyspacelines.com, which I believe was to be the operator. Actual website became defunct a few years ago.

 

[FutureSpaceTourist]

Here are some further images; it's a shame that the artist impression ones are so small. Still reminds me of SpaceShipTwo!

 

[RanulfC]

Not sure, but I seem to recall that this wasn't actually a "two-stage" suborbital system but a suborbital jet-rocket with a later to be "added" supersonic carrier aircraft for a fully orbital system.

The Vela had jets and rockets for a normal airport take off and landing but the carrier would later allow a supersonic launch of the Vela for true orbital capability.

Randy

 

[FutureSpaceTourist]

The flight profile (attached three posts ago) does seem to say that it is two sub-orbital stages. I agree that jets on the space cruiser seem overkill, although I suspect they wanted a powered landing rather than a glide. There just doesn't seem to be large enough tanks on the space cruiser to have the propellants needed for orbital velocity.

 

[FutureSpaceTourist]

I'd wondered what happened to Vela / Space Cruiser, although I assumed it was a funding issue. Then recently I found this from a 2000 Forbes article:

[quote author=http://www.forbes.com/global/2000/0207/0303094a_print.html]
Vela Technology Development of Vienna, Virginia, is developing the Space Cruiser--a fully reusable, two-stage rocket. Its president, Charles (Pat) Kelley, 55, a former aerospace engineer with the U.S. Air Force and a consultant on antiballistic missiles to the Department of Defense, figures that he can make money if Space Cruiser carries at least six passengers at $80,000 a head (net of booking commissions).

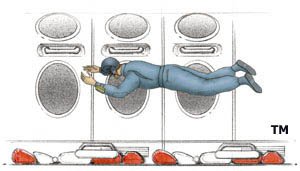
Kelley is focusing on passenger comfort. Because the Cruiser would go only suborbital, the maximum force on passengers would be two Gs. That's less than the amount produced by a roller coaster and will make flights accessible to a wide range of people. (NASA's Space Shuttle maxes out at around four Gs.) Plans call for a "Sky Lifter" plane to carry the Cruiser, which looks and lands like a futuristic airplane, to 12 kilometers up and launch it in midair.

A lot of this is still pie in the sky, however. Kelley is trying to raise $150 million and is in discussions with some deep-pocketed potential investors. But so far he has raised only $1 million. [my emphasis]
[/quote]

Same old story.