Northrop XST

[hesham]

The 1979 sketch from that article that Scott reckoned he's seen before was in the 1991 AIAA article 91-3069 "Technology in the lives of an Aircraft Designer" by Irv Waaland. I think this was the first time the Northrop XST was depicted, too.

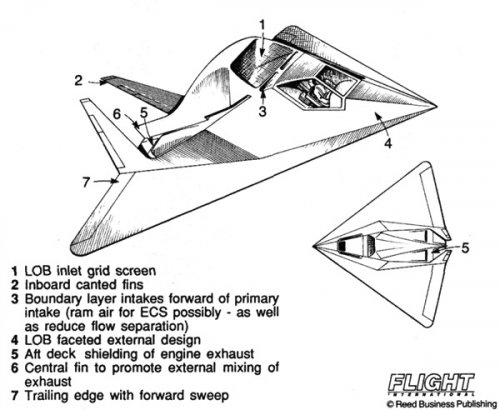
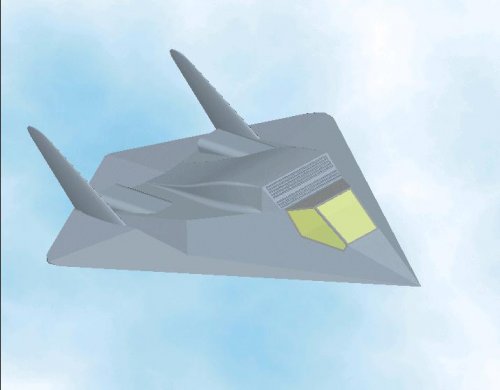
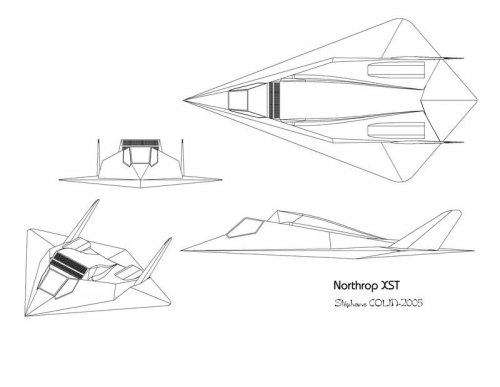
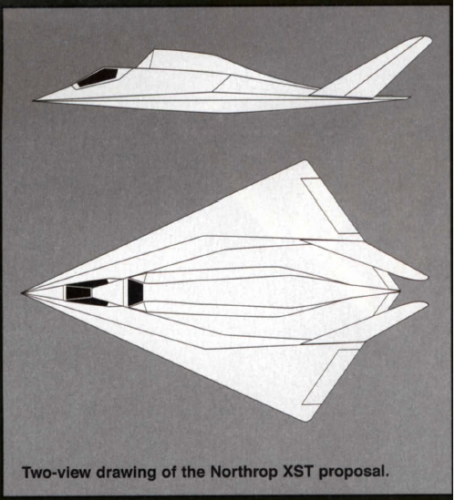
The Northrop XST;
http://www.flightglobal.com/FlightPDFArchive/1992/1992%20-%200362.pdf

 

[Matej]

I don't know why it is so secret till now. Any of my attempts to get a 3 view of this plane failed.

 

[flateric]

http://www.amazon.com/F-117-Nighthawk-Stealth-Fighter-Scrapbook/sim/158007099X/1

F-117 Nighthawk Stealth Fighter Photo Scrapbook (Paperback)
by Yancy Mailes (Author), Tony R. Landis (Author) - has 3-view

FI drawings are based on Northrop artist's impression and has absolutely incorrect proportions.

 

[Matej]

And accuracy? When I remeber correctly, I have one, but only extracted and computed from the illustration and RCS model. I tried to obtain original 3 view from Northrop.

 

[flateric]

Tony's drawings are based on XST factory desktop model and quite accurate.

 

[Matej]

Well, then I included this book to my wish list. Thanks for the tip.

 

[Antonio]

Thanks for the advise Flateric, I added a copy to my wish list too

 

[roadrunner2]

hello, is it possible to see the 3 view....

long time ago I've do this:
it's a 3d model I made to help scratchbuilding a 1/72 model kit.
I think it's totaly wrong :-\

 

[flateric]

Not so bad result, but you must be next buyer of

http://www.amazon.com/F-117-Nighthawk-Stealth-Fighter-Scrapbook/sim/158007099X/1

this will reveal some details)

 

[Matej]

It must be this:

 

[Orionblamblam]

Today I received an unfinished 1/72 Northrop XST model from a well-placed source. This model was one of some number produced at the Northrop model shop. My plan is to clean it up (already in process) and make a mold of it, and cast a dozen or two copies of it just the way it is. Then take one of those copies and re-work it to be more detailed and accurate, and make copies of *that.*

 

[CFE]

Looks pretty groovy. Good find!

 

[frank]

Looks like something to put on my want list!

Today I received an unfinished 1/72 Northrop XST model from a well-placed source. This model was one of some number produced at the Northrop model shop. My plan is to clean it up (already in process) and make a mold of it, and cast a dozen or two copies of it just the way it is. Then take one of those copies and re-work it to be more detailed and accurate, and make copies of *that.*

 

[aim9xray]

http://www.ebay.com/itm/281228147544

 

[overscan (PaulMM)]

Been watching that one, wondering if one of our collectors would buy it.


Nice model.

 

[hesham]

Hi,


I found those two drawings to Northrop XST in my files.

 

[allysonca]

From my collection. Interesting to note that the base is a YF23 base with a new plaque. I made 10,000 YF-23's for Northrop and there were a few bases laying around I guess. Enjoy!

 

[hesham]

Nice Model Allysonca.

 

[ghostmodeler]

Allyson, it shouldn't be a surprise the XST has a YF-23 base...thanks to you we had a ton of those readily available in the shop and it fit the model nicely.

 

[Hobbes]

10,000? Bloody hell.

 

[Ian33]

10,000? Bloody hell.

Guess Northrop was going to give every one when they won the ATF fly off. Dammit... The XST though would be a delight to see if they can find it!!

 

[ikke666]

any-one any idea of the seize of the northrop xst? (length, span and height) ? :

 

[Empire]

This is the N-327 RCS pole model. Where dose it fall in relation to the final pole model tested in the XST pole off with lockheed? What was the N number for the final pole model tested?

 

[Apollo Leader]

For those who have read the N-327 and N-335 sections of Tony Chong's Flying Wings and Radical Things, the work on N-327 led to Northrop's final XST design. N-335 is a mystery on whether it was Northrop's internal design number for its final XST entry or possibly the design number given to the RCS pole that Northrop designed to mount both Northrop's and Lockheed's XST models.

 

[Grey Havoc]

By the way, the result of one of our fellow members hard work which has been out for a while:

Northrop XST 1:72 Resin Model by Fantastic Plastic

A 1:72 resin model kit of the Northrop XST stealth technology demonstrator by Fantastic Plastic Models

fantastic-plastic.com