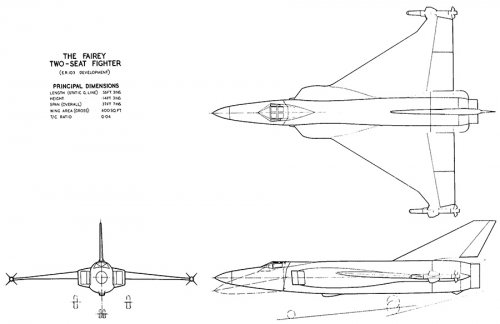
Fairey ER.103 fighters

[PMN1]

Does anyone have information on the ER.103B and C fighter proposals and how would they have compared to the aircraft around and in development at the time?

 

[overscan (PaulMM)]

I've got nothing more than what is in Project Cancelled and BSP:Jet Fighters on ER.103B/C. I have a lot of information on the subsequent derivative offered to F155T (the non-compliant alternative to the Delta III) if thats of interest.

 

[lark]

There is also an excellent two part article
'Fairey Delta Fighters' by W.A.Harrison in
Aircraft Illustrated of November and December 1984
which gives data of the three Fairey E.R103(FD2) Developments.

 

[overscan (PaulMM)]

F155T (ER.103 development)

 

[overscan (PaulMM)]

From Project Cancelled, ER.103C

 

[PMN1]

I've got nothing more than what is in Project Cancelled and BSP:Jet Fighters on ER.103B/C. I have a lot of information on the subsequent derivative offered to F155T (the non-compliant alternative to the Delta III) if thats of interest.

Its the Project Cancelled chapter that has got me wondering how they would have compared to the Mirage........and how the Mirage would have fared had Fairey not needed to move testing of the Delta II to France as a result of noise abatement rules.

 

[alertken]

how the Mirage would have fared: Cross-refer to thread Mirage III genesis, esp. Overscan's post #12.

MoS, 1954/55 perceived Fairey as overloaded in management (Heston GW was particularly under-resourced), as unfocussed in design, bidding widely - helicopters, deltas, civil ambition that evolved as team member for (to be DH.121), and as slothful in production at Stockport and Hayes of Gannet AS.1/4, embarrassing as much MSP-money had been extracted for this crucial type. Buttler,P.84 quotes Fairey as considering ER.103 FD.2 derivatives to be "the best combination (for 1960) capable of much development". Really? RAE/MoS did not agree. If Sandys had not sensibly reduced the high altitude interception task, and if the Fairey F.155T bid (beauteous cover of Buttler/1) had attracted favour, he would have picked up the merger shotgun that was revealed for TSR.2 in 1959.

 

[overscan (PaulMM)]

* MD.550 - Mach 1.15 in shallow dive. Drag way too high for the limited thrust.
* Fairey Aviation provided FD2 data to Dassault, as a result MD.550 fin and dorsal spine redesigned, length and wingspan reduced slightly.
* Renamed Mirage I. Speed increased to Mach 1.3 in level flight with rocket boost
* Mirage II was a larger development with a larger wing based on Fairey data and two Turbomeca Gabizo turbojets. Not built.
* Mirage III (01) had almost identical wing to the Mirage II project, but new "area-ruled" fuselage based on US research. SNECMA Atar 101G.2 turbojet. Mach 1.52 in level flight.
* Refitted with conical "shock cones" similar to the F-104, achieves Mach 1.6 (jet engine) and Mach 1.9 (with rocket boost).
* Mirage IIIA - increased thrust Atar 9B, wing redesigned to reduce drag and increase lift. Conical leading edge camber adopted [as recommended by NASA Ames research and implemented on F-106 and B-58]. Mach 2 reached.

As you can see, Fairey research was useful, but not the whole story.

Crosspost from Mirage III Genesis topic...

 

[overscan (PaulMM)]

I agree - the flights were a non-issue, Fairey's assistance was earlier and much more direct. It also was only a small part of the Mirage design: the NASA wing profile and area ruling concepts were much more important in the end.

 

[overscan (PaulMM)]

There is also an excellent two part article
'Fairey Delta Fighters' by W.A.Harrison in
Aircraft Illustrated of November and December 1984
which gives data of the three Fairey E.R103(FD2) Developments.

Ordered December on Ebay, still looking for November.

 

[alertken]

The reason we all cross-fertilised in 1951/53 was we were all facing one enemy. Area rule, whatever, was shared to expedite putting fit kit in NATO hands to deal with an imminent Threat. Exports, making money was not a factor. And if anyone has a right to moan about "copying" it's the US taxpayer, whose MSP $ tooled Dassault (and funded many Mystere IVA), Fairey (for Gannet)...et al. MSP was the Mutual Security Program.

 

[PMN1]

Ok, so the timing suggests that Dassault got little if anything from the FDII tests, but could the 103B have been developed into a Mirage equivalent?

Derek Wood goes onto say 'It is recorded in Mirage, Warplane of the World by Jack Dee that 'later when the Mirage was conquering markets all over the world, Dassault told a British aircraft chief, "If it were not for the clumsy way in which you tackle things in Britain, you could have made the Mirage yourselves".'

 

[TinWing]

The reason we all cross-fertilised in 1951/53 was we were all facing one enemy. Area rule, whatever, was shared to expedite putting fit kit in NATO hands to deal with an imminent Threat. Exports, making money was not a factor. And if anyone has a right to moan about "copying" it's the US taxpayer, whose MSP $ tooled Dassault (and funded many Mystere IVA), Fairey (for Gannet)...et al. MSP was the Mutual Security Program.

Most people have forgotten that the U.S. flooded the Western European aviation sector with monetary and technical aid during the Eisenhower era. There were many practical considerations, such as maintaining employment to forestall the advance of communist trade unions, as well as maintaining access to then superior British gas turbine technology. Without American dollars, it is doubtful that the Hawker Hunter would have been produced in such great numbers, or that the Blackburn Buccaneer would have been produced at all.

The crisis in the British aviation sector started when American funding started to dry up in the 1960s. Just as costs and performance requirements escalated, the largely disinterested British taxpayer was forced to shoulder an increasingly heavy burden for military aircraft procurement. France avoided the same disasterous spiral by embracing less ambitious requirements and generating useful export markets.

 

[TinWing]

Ok, so the timing suggests that Dassault got little if anything from the FDII tests, but could the 103B have been developed into a Mirage equivalent?

Derek Wood goes onto say 'It is recorded in Mirage, Warplane of the World by Jack Dee that 'later when the Mirage was conquering markets all over the world, Dassault told a British aircraft chief, "If it were not for the clumsy way in which you tackle things in Britain, you could have made the Mirage yourselves".'

A large Gyron engined Fairey Delta derivative would have lacked the export potential of the far smaller, far cheaper ATAR powered Mirage III. The Gyron was very much in the same class as the American J-75, which would have placed the production Fairey Delta in the same general category as the American F-105 and F-106 - and as you are well aware, neither fighter had any export success either.

I personally would argue that the Avon 200 was superior to the contemporary ATAR, and that Fairey was entirely capable of productionizing the FDII, although the military, political and commercial motivations for such a development were entirely absent. In hindsight, a single Avon powered delta equivilent in size and performance to the Mirage III would have made tremendous sense, but......

 

[overscan (PaulMM)]

It would be technically feasible, but the RAF in the mid 1950s was too intent on getting something better than whatever the US had to settle for something like the Mirage.

 

[PMN1]

I personally would argue that the Avon 200 was superior to the contemporary ATAR, and that Fairey was entirely capable of productionizing the FDII, although the military, political and commercial motivations for such a development were entirely absent. In hindsight, a single Avon powered delta equivilent in size and performance to the Mirage III would have made tremendous sense, but......

Derek Woods does go on to say as a competitor to the F-104G for Germany, Dassault, Fairey and Rolls Royce offered a collaborative venture as an alternative. The wings were to be built by Dassault, the fuselage by Fairey and RR would provide a re-heated Spey. Belgium were to have been involved as well in the manufacturing programme as well but the F104G won the day.

 

[TinWing]

Derek Woods does go on to say as a competitor to the F-104G for Germany, Dassault, Fairey and Rolls Royce offered a collaborative venture as an alternative. The wings were to be built by Dassault, the fuselage by Fairey and RR would provide a re-heated Spey. Belgium were to have been involved as well in the manufacturing programme as well but the F104G won the day.

Nothing else has come to light as far as the F-104 competitor, although I suspect that Lockheed had a very...uh....generous....sales pitch.

 

[overscan (PaulMM)]

From W A Harrison's article in Aircraft Illustrated December 1984

 

[overscan (PaulMM)]

Better version?

 

[Lascaris]

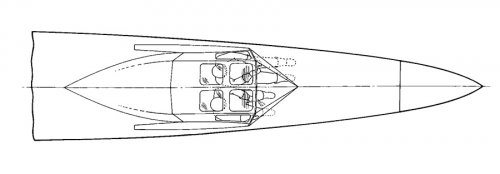
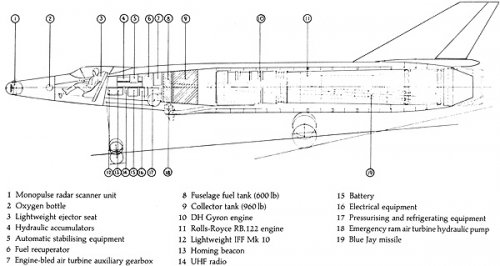
Am I understanding correctly that ER.103B is supposed to be roughly the same size of a Mirage III and the same weight (20650 to about 21000) but with twice the thrust at 27.000 lbf? Which gives it a thrust to weight ratio over 1 without afterburning? How practical was that?

 

[overscan (PaulMM)]

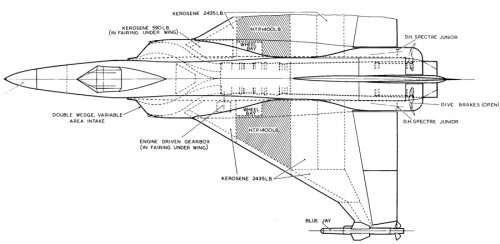
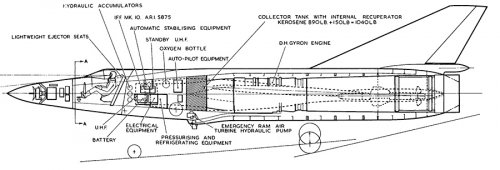
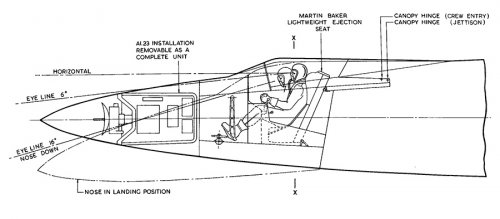
ER103B was a high speed research aircraft with no equipment, weapons or much fuel, so not a practical fighter.


ER103C was supposed to be a fighter. Early Gyrons were rated at about 24,000lb, which would be reasonable, adding the rockets would make it pretty hot. Mirage III had one of the worst thrust/weight ratios of its generation due to the rather old fashioned Atar engine, The Lightning had a high thrust to weight ratio, ER103C would have been at the Lightning end.

 

[MilwaukeeRoad]

* MD.550 - Mach 1.15 in shallow dive. Drag way too high for the limited thrust.
* Fairey Aviation provided FD2 data to Dassault, as a result MD.550 fin and dorsal spine redesigned, length and wingspan reduced slightly.
* Renamed Mirage I. Speed increased to Mach 1.3 in level flight with rocket boost
* Mirage II was a larger development with a larger wing based on Fairey data and two Turbomeca Gabizo turbojets. Not built.
* Mirage III (01) had almost identical wing to the Mirage II project, but new "area-ruled" fuselage based on US research. SNECMA Atar 101G.2 turbojet. Mach 1.52 in level flight.
* Refitted with conical "shock cones" similar to the F-104, achieves Mach 1.6 (jet engine) and Mach 1.9 (with rocket boost).
* Mirage IIIA - increased thrust Atar 9B, wing redesigned to reduce drag and increase lift. Conical leading edge camber adopted [as recommended by NASA Ames research and implemented on F-106 and B-58]. Mach 2 reached.

As you can see, Fairey research was useful, but not the whole story.

Crosspost from Mirage III Genesis topic...

As far as can be seen, the Mirage III is the only aircraft in this entire forum where you have taken the trouble to trace any possible contribution from every possible source from countries or builders other than the ones it came from. There are litteraly pages devoted to British and American aircraft of the same era, that benefited tremendously from German aerodynamical research in WWII, but this fact is hardly if ever mentionned. How do you explain and justify that the Mirage III, Dassault products generally and, more widely, other aircraft and pieces of harware of the same origin get this singular treatement (there was even a recent post by "Alterken", which linked -no kidding, apparently-, the American (liquid-fuel) Thor IRBM technology of the 1950s and de Gaulle with Hades, a late-80s solid-fuel SRBM!).

 

[Lascaris]

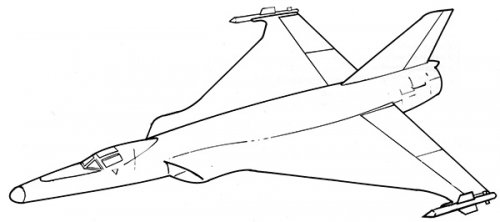
I understand for the British secret projects book that Fairey was proposing two different fighter developments of the Delta 2? ER-103B with the same wing (expected to need 18 months to first flight) and ER-103C with a cranked delta wing (expected to need 30 months) to first flight?

Both seem to be from somewhat (103B to quite a bit (103C) larger than a Mirage III as well?

ER103B was a high speed research aircraft with no equipment, weapons or much fuel, so not a practical fighter.


ER103C was supposed to be a fighter. Early Gyrons were rated at about 24,000lb, which would be reasonable, adding the rockets would make it pretty hot. Mirage III had one of the worst thrust/weight ratios of its generation due to the rather old fashioned Atar engine, The Lightning had a high thrust to weight ratio, ER103C would have been at the Lightning end.

 

[alertken]

MWR: (IIRC) what (I hope) I said was that Atlas/Thor informed Blue Streak, which became Stage 1 of ELDO Europa, which, 29/3/62, C CDG joined “(against) advice of all the experts” M.deMaria/J.Krige,European Attempts in Launcher Technology, History & Technology Journal, 92/9,P.11. That gave France access through DH to US’ IC/IRBM data* (and so will have been a step onway to Hades).

I don't think Mod. is having a go at France: he, me, others here simply emphasise the interdependence of aero-technology progress. I, others, dislike anyone's efforts to claim "ownership" of, well, anything really. There's a continuum. Where would the Rolling Stones have been without obscure Bluesmen (/girls) paving the way? (* or, as US comedian Bob Hope said of Sputnik, 1957: "so, what does that prove...that (USSR's) Germans are better than our Germans" {and I cannot "own" that bon mot of my fellow Londoner - he was born in Eltham}).

 

[overscan (PaulMM)]

* MD.550 - Mach 1.15 in shallow dive. Drag way too high for the limited thrust.
* Fairey Aviation provided FD2 data to Dassault, as a result MD.550 fin and dorsal spine redesigned, length and wingspan reduced slightly.
* Renamed Mirage I. Speed increased to Mach 1.3 in level flight with rocket boost
* Mirage II was a larger development with a larger wing based on Fairey data and two Turbomeca Gabizo turbojets. Not built.
* Mirage III (01) had almost identical wing to the Mirage II project, but new "area-ruled" fuselage based on US research. SNECMA Atar 101G.2 turbojet. Mach 1.52 in level flight.
* Refitted with conical "shock cones" similar to the F-104, achieves Mach 1.6 (jet engine) and Mach 1.9 (with rocket boost).
* Mirage IIIA - increased thrust Atar 9B, wing redesigned to reduce drag and increase lift. Conical leading edge camber adopted [as recommended by NASA Ames research and implemented on F-106 and B-58]. Mach 2 reached.

As you can see, Fairey research was useful, but not the whole story.

Crosspost from Mirage III Genesis topic...

As far as can be seen, the Mirage III is the only aircraft in this entire forum where you have taken the trouble to trace any possible contribution from every possible source from countries or builders other than the ones it came from. There are litteraly pages devoted to British and American aircraft of the same era, that benefited tremendously from German aerodynamical research in WWII, but this fact is hardly if ever mentionned. How do you explain and justify that the Mirage III, Dassault products generally and, more widely, other aircraft and pieces of harware of the same origin get this singular treatement (there was even a recent post by "Alterken", which linked -no kidding, apparently-, the American (liquid-fuel) Thor IRBM technology of the 1950s and de Gaulle with Hades, a late-80s solid-fuel SRBM!).

I don't understand your point exactly, but I was trying to disprove the (British) idea that the Mirage III owed a large technical debt to Fairey. Every aircraft designer in the world was reading research reports and studying rival designs from various countries for interesting developments. I don't think the Mirage III was particularly revolutionary, but it was certainly successful by any measure.

 

[ivran]

ANY information or data for this projects

 

[ivran]

and this ER.D

 

[hesham]

Nice drawings Ivran,

but what is you source ?, Air Enthusiast magazine ?.

 

[CJGibson]

More to the point, why put a 70-degree delta on a transonic aircraft?

Chris

 

[ivran]

Pictures are from some magazines, but Y not saved any details, now try to find data or information

best regards

 

[fightingirish]

Probably these pictures are from:

Beyond the Frontiers: Fairey Deltas – FD.1, FD.2 & BAC 221
Article by Jon Lake
Illustrations by William "Bill" Harrison
Wings of Fame Volume 11
Aerospace Publishing 1998, ISBN: 1861840187

Sorry, I was wrong! :-[

 

[CNH]

"That gave France access through DH to US’ IC/IRBM data* "

Blue Streak and the French missile programme had almost nothing in common.

 

[Hood]

I've not seen those Fairey Delta variants before.
I'm with Chris in that the Transonic Research version would seem to be pretty 'hot' for such work and would seem more likely to be for highish Mach numbers (M2-2.5?). At first I thought it might have been an older Delta II concept but the design seems too advanced and refined from the Delta II for that hypothesis to stand up.

 

[ivran]

this view is from same source, unknown report, y will found this information and drawing,

 

[ivran]

and this view, source is known, only for this pictures, at the this moment

 

[hesham]

Hi Ivran,

I think Air International or Flying Review are the suggesting magazines,can you remember more please ?.

 

[overscan (PaulMM)]

Looks like Air Enthusiast to me.

 

[hesham]

Nice drawings Ivran,

but what is you source ?, Air Enthusiast magazine ?.

As I suggested before my dear Paul,but he didn't remember the source ?.

 

[ivran]

picture Fairey Delta 2, with two Napier sabre ram jet, from book British secret projects. hypersonics ramjets ... from Tony Buttler and Chris Gibson
other two pictures, y will found sources in my archive,

 

[hesham]

OK Ivran,

but I think the other drawings never goes far those magazines;

- Air Enthusiast
- Air Pictorial
- Air International
- Flying Review