Douglas DC-4 Bomber developments

L

lark

ACCESS: Top Secret
Senior Member
Joined
17 February 2006
Messages
1,862
Reaction score
278
In an article by René Francillon for Air Magazine N°47-Octobre 2009
mention is made of a bomber development of the Douglas DC-4E liner
under the designation DB-4.

This design was offered to the U.S.Army Air Corps in 1938 to replace
the XB-19 who was already almost outdated at that time.

Is there anyone who haves more information or illustrations..

Thanks in advance.
 
lark said:
In an article by René Francillon for Air Magazine N°47-Octobre 2009
mention is made of a bomber development of the Douglas DC-4E liner
under the designation DB-4.

This design was offered to the U.S.Army Air Corps in 1938 to replace
the XB-19 who was already almost outdated at that time.

Is there anyone who haves more information or illustrations..

Thanks in advance.

Did the DC-4E was acquired by Japan in order to obtain a bomber??
Click to expand...
 
The Nakajima G5N1 who was based on DC-4E technology has nothing
to do with the planned DB-4...

This should have been a entirely different design.
By the way , in Air Classics , mention is made that the
initial concept for the XB-19 should have been a six engined design.
Maybe this is related to the Douglas 6 engined bomber in the 'US bombers' thread.
 
Hmm. I've mentioned before that I've read somewhere that Douglas had offered a bomber version of the DC-4 in their designs for the XB-31. This has me wondering if they meant the DC-4E!


lark said:
In an article by René Francillon for Air Magazine N°47-Octobre 2009
mention is made of a bomber development of the Douglas DC-4E liner
under the designation DB-4.

This design was offered to the U.S.Army Air Corps in 1938 to replace
the XB-19 who was already almost outdated at that time.

Is there anyone who haves more information or illustrations..

Thanks in advance.
Click to expand...
 
any pics of original Douglas DB-4 ?

here and below link and images of Nakajima G5N Shinzan born by project of Douglas DC-4E (
http://www.j-aircraft.com/gallery/navy/g5n_gallery/g5n-peter_fearis_01l.jpg
 

Attachments

  • g5n-peter_fearis_01l.jpg
    g5n-peter_fearis_01l.jpg
    31.8 KB · Views: 777
lark said:
In an article by René Francillon for Air Magazine N°47-Octobre 2009
mention is made of a bomber development of the Douglas DC-4E liner
under the designation DB-4.
Click to expand...

Surprising since the DB-4 designation had already been given to the B-18A Bolo.
I'm not saying this is impossible, however, considering the DC-4, DC-7 and DC-8 designations were all re-allocated to newer designs.

See here for the bomber development of the first DC-4:
http://www.secretprojects.co.uk/forum/index.php/topic,488.msg157967.html#msg157967
 
The Douglas DB-4 design, together with the Boeing Y1B-20
are mentioned as follow on designs for the XB-15
by Bill Norton in his brilliant new book

"American Bomber Development in WW 2" ....
 
I have posted an article on the Douglas DC-4 bomber version -- NOT that of the DC-4E -- over on Hyperscale, along with drawings and downloadable 1/72nd scale drawings of same.

I invite you to go have a look.

AlanG
 
Great!, I'd love to take a look.
Where can we find it? : link, reference...

Thanks a lot,
 
Very interesting piece Alan.

In late 1941/early 42 The Admiralty suggested that a variant of the DC-4 be used as a very long range reconnaissance (VLR) aircraft, fitting it with ASV and racks for 12 x 250lb depth bombs to make C-54 GRs (General Reconnaissance, RAF designation for maritime patrol types in WW2). They were to be used out of Bathurst, the Azores and Gibraltar, away from German fighters, as they would not be fitted with defensive armament. The Admiralty sticking its oar in (sorry) to Air Staff business prompted some 'fruity' correspondence. The Air Staff said that the lack of flak suppression guns was the main problem but I suspect it was inter-service rivalry. Full story is in Nimrod's Genesis. (Pg 98)

Chris
 
Last edited by a moderator:
In 1939 the DC-4 was also suggested as a suitable lower component for a civil Mayo composite aircraft carrying a new high-speed, long distance, upper component aircraft of 32,000lb gross weight. Although not specified in the note military application would have been considered too, Mayo made many such proposals around this time.
 
Thank you all for the kind remarks. I'm glad you liked the article. I very big thanks to CJGibson and Schneiderman for the additional historical background information. I feel a purchase of Nimrod's Genesis coming on....

To answer Maveric, I have not yet found the Douglas model number for this aircraft. The logical place to look would be at the Douglas Archives, of course, but getting information out of there has proven to be a nearly impossible task, unfortunately.

Thanks again. As I find more information I shall share it.

Watch the skies!

AlanG
 
Nice find my dear Paul.
 

Attachments

  • Illustration 1 DC-4 Bomber TOP & SIDE with WINGS.jpg
    Illustration 1 DC-4 Bomber TOP & SIDE with WINGS.jpg
    60.1 KB · Views: 423
  • Illustration 2 DC-4 bomber SIDE and Inboard Profiles.jpg
    Illustration 2 DC-4 bomber SIDE and Inboard Profiles.jpg
    84.2 KB · Views: 417
What a strange proposal, it seems like the sort of design that could only come about in the immediate prewar period when the priority was to get something into production to fill in the want of equipment.

What size are the largest bombs, 1000 lbs? If so it would have, what, a 4000 lb total bomb load?
 
Think this was not a Douglas idea but one
proposed by Fokker in The Netherlands who had
a Douglas licence for the DC-3...
 
Depending upon how you look at it, the USAAAF DID have something of a kinda sorta DC-3 bomber - the B-18. Certainly not much of a combat aircraft, but it did provide a lot of pilots with multi-engine time before graduating to the true combat aircraft like the B-17, etc., and provided a good, stable platform for coastal anti-submarine patrols early in the war.

AlanG
 
Yes indeed. And as far as I know (and read) Douglas did also some designwork for bombers
based on their DC-1 and DC-5 civil transports.
 
ACResearcher said:
Depending upon how you look at it, the USAAAF DID have something of a kinda sorta DC-3 bomber - the B-18. Certainly not much of a combat aircraft, but it did provide a lot of pilots with multi-engine time before graduating to the true combat aircraft like the B-17, etc., and provided a good, stable platform for coastal anti-submarine patrols early in the war.

AlanG
Click to expand...

My grandfather flew in a B-18 a couple times and his memory of it was that, while he was fooling around in the dorsal turret the pilot called back to tell him to knock it off because it was effecting the plane's flight characteristics!
 
Interesting feedback so far on my article.

After seeing Hesham's post of my drawings (yes, I did them), I feel like I should once again let people know that there are downloadable 1/72 scale copies of the drawings linked in the article over on Hyperscale. http://www.clubhyper.com/reference/dc4bomberag_1.htm

Sherman, I have no data on bomb loadouts or capacity, nor do I have much hope of being able to get them out of Douglas, but since the standard load of the time appears to have been 2000lbs, I'd guess that was what it was designed around. That's the way the ball bounces in research. That's a great story about your grandfather, and not a surprise, either. The U.S. was miles behind in terms of turret research prior to WWII, and the aerodymanics of that B-18 top turret had to be roughly equal to putting up a sail. Reading the data on the complaints about the various U.S. turrets once the war started is illuminating to say the least. Of all the aircraft-mounted turrets, my own opinion is that the Martin A-3 series has to be one of the best and was upgraded throughout the war. And the Sperry ball turret was THE best belly turret, shown in part by the survival rate among those gunners.

Alan
 
ACResearcher said:
Of all the aircraft-mounted turrets, my own opinion is that ... the Sperry ball turret was THE best belly turret, shown in part by the survival rate among those gunners.

Alan
Click to expand...

True. But they were not infallible. Hence, one of the finest and most famous war poems of all times:

The Death of the Ball Turret Gunner - Wikipedia

en.wikipedia.org en.wikipedia.org

See also his collections Little Friend, Little Friend and Losses.

The personal cost of war is something to remember on this U.S. Veterans Day.
 
Dear ACR.

In your article about the DC-4 bomber version, you mention
the DC-4E bomber variant and a future book.

Can you tell us a bit more about this book if possible ?
Thanks in advance.

L.
 
Lark,

I hope you enjoyed the article on the DC-4 bomber.

I'd love to tell you more about the project in which the DC-4E bomber will appear, but for one thing it is at least a couple years away (although I've been researching it for at least five years) and I'm hesitant to reveal too much as there are frankly too many folks who cannot be trusted. Tell you what...drop me an email and we'll go from there.

ag122651 at hotmail dot com

AlanG
 
There is a great article about this topic in the new issue 28 of "The Aviation Historian".

"we examine the – ultimately fruitless – attempts to turn Douglas’s DC-4E airliner and its smaller brother the DC-4/C-54 into bombers"
 
I do hope you will all get a copy of the latest "The Aviation Historian", Issue 28. In it I recount what is - and may well remain so - the most complete history of the attempts to make the DC-4E and, eventually, the DC-4 into bombers.

In the meantime I shall correct some errors in Bill Norton's book. The DB-4/DC-4E bomber design did indeed come AFTER the Y1B-20, but was not exactly a "follow on" Project. The DC-4E bomber was Douglas' entry into CP 39-645, a relatively hastily written Emergency Proposal to basically jump through the right hoops so the AAF could order the B-24, a decision they had already made. It is my belief that Douglas submitted this bomber version in order to recoup its investment in the DC-4 (as it was then known) due to the fact that once the prototype was built all the airlines that had participated in its design and building summarily rejected it. The reasons for this, as well as the AAF's engineering reports on both the DB-4 and the DC-4/DS-300 bomber submissions, are all lovingly recounted from the original AAF documents in this new article, including a number of new drawings of both. It was - to me - a fascinating story of virtually unknown (and generally badly researched) aircraft projects.

I hope you will enjoy reading the article as much as I enjoyed writing and illustrating it. I have to hand it to the chaps at TAH for the beautiful job of layout they did. They are true pros.

Submitted for your consideration,

AlanG
 
I have a copy of picture to a Model for this Project,but the scanner is out of service now.
 
The Aviation Historian article on the various efforts to build a bomber out of the DC-4E and DC-4 is indeed very interesting.

I have one question though, in the recent American Secret Projects Vol.2 there is a brief description of a couple of other DC-4 bombers on p.33 that look very similar but are more 'basic' conversions with a ventral gondola for the bombs and/or the bomb-aimer. Where do these studies fit into the story? I assume these were slightly earlier than the definite DS-412 design covered in depth in the article?
 
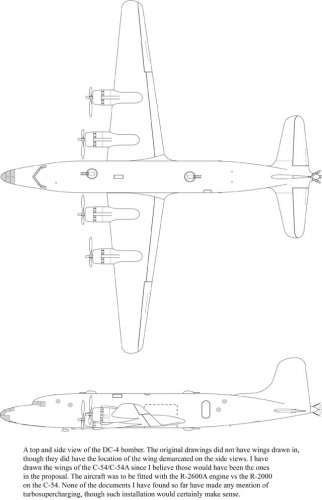
Hood,

This is one of the "joys" of research!

Craig Kaston, one of the authors of ASPII, came up with those two versions in a source to which I have no access. I came up with my drawings from a source to which HE had no access. THe story of the DC-4E bomber was gathered by me through in-depth (and VERY lucky) research at NARA II in a file I had pulled mostly in desperation and of which Craig had no knowledge at all. Craig has to get permission from his source before I can officially have access to his drawings and any materials accompanying them.

In the meantime, I have come across an entry for the DC-4E bomber in a Type Specification dating from March, 1938, nearly two years before CP 39-645. This brings up TONS of questions yet to be answered: I assume it was an entry of the same configuration seen in 39-645, but maybe not. If so, did the AAF just throw it into the consideration on 645 because they then had three complete proposals with one to toss so they could choose both the B-24 and the Boeing entries which were newer versions of the B-17? The Type Specification mentioned earlier has a TON of entrees, including one from Sikorsky and one from the Materiel Division. The drawings accompanying all the entries are listed in the documents, but are not IN the documents, and no one seems to have any idea where they might be. One of the Boeing entrees is for a Model 299G. What in the devil is a Model 299G? Still no word from Boeing.

This is not really anything new among serious researchers and it just takes time to gather everything. The "gatherers" who seem to write most of the books and monographs will just steal this info and use it in one of their missives, almost never crediting their sources. One sees that a lot on HERE, too.

Anyway, I hope this answers your question as this is all the information there is to date (that I'm wiling to share) about what has transpired.

AlanG
 
Last edited:
That is indeed the joy of research, especially when things are scattered in different archives and locations. Every unexpected find leads to more questions, I've had that experience several times too.
The definitive story is always a never-ending hope just tantalisingly out of reach.
There are early plans afoot here in Britain to create a central aviation archive which The National Archives seem to be advising on. Whether it will ever happen is open to question, but if it ever did come off then it would make research a lot easier. What worries me is the loss of expertise, every archive has its band of custodians who often have direct knowledge and experience and those guys are getting no younger. In twenty years time we might be all the poorer for the loss of knowledge they have about their archives and the contents.
 
Hood said:
…….There are early plans afoot here in Britain to create a central aviation archive which The National Archives seem to be advising on. Whether it will ever happen is open to question...…..
Click to expand...
Interesting. Given the large number of archives in the country, and the variable ease of access to these, it will be a task of epic proportion. I wish whoever is leading this the very best of luck and they have my full support, for what it is worth. I am a volunteer at the Royal Aero Club Trust archive which contains a significant amount of material relating to aircraft and projects unrelated to the Club and I am slowly drawing this together in a catalogue, of sorts.
 

Similar threads

Please donate to support the forum.

Back
Top Bottom