de Havilland four-engined fast bomber

P

PMN1

ACCESS: Top Secret
Senior Member
Joined
4 June 2006
Messages
1,254
Reaction score
1,246
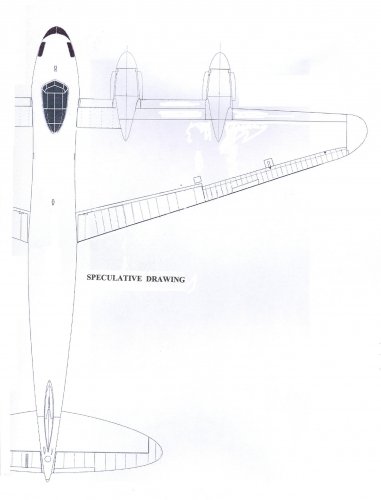
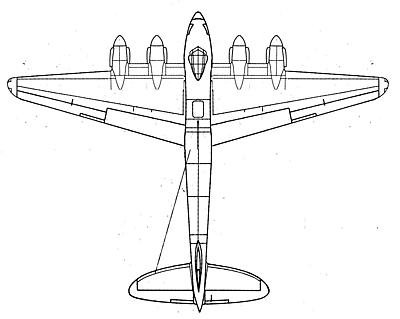
From Tony Buttler’s ‘British Secret Projects, Fighter and Bombers 1935 –1950.

‘De Haviland also studied a development of the Mosquito with four Merlins as a ‘fast’ heavy bomber but the general arrangement drawing known to have been produced has not been found. In 1941 the company did put forward a design for a high-speed unarmed night bomber which was a fairly big aircraft of around 46,000lb (20,866kg) weight, and it seems pretty certain that these were the same project.’


Does anyone know if anything has turned up on this since the book was published?
 
Thanks PMN1
I would definitely like a look at this if anything materialises.

I would imagine it would be somewhat bigger. Wings extended to accommodate the extra pair of Merlins and probably an longer fuselage etc.
If I can get a concensus of opinion, I may even attempt a profile, just to see what may have been possible.
Educated guess kind of thing, and of course, suitably labelled.

Cheers
Peter
:p
 
Hi,

I think just a fake aircraft.
http://rareaircraf1.greyfalcon.us/GREAT%20BRITAIN.htm
 

Attachments

  • ae35.jpg
    ae35.jpg
    51.6 KB · Views: 649
Well, I always wondered why they didn't try to turn the Albatross (or whatever it was?) into a bomber, then I remember reading somewhere that they did and it didn't turn out so great.
 
Out of interest, any ideas on what an Albatross with four Merlins would do?
 
"Albatross suffered stuctural failures ..."
That photo looks similar to several others showing Fw 200 Condors, another type, which
was (ab-)used as a make-shift bomber.
Was there ever a succesful bomber design derived directly from a passenger aircraft ?
The only one I can think of in the moment is the B-18, but I don't know, if there was more
than a superficial resemblance left with the DC2 in the end.
 
the albatross`s structural problems come from the window openings. there was also an attempt to build abomber version that ultimately led to the mosquito.
 
4 Merlins vs 4 Gipsy engines should give quite a bit of extra power for beefing up the structure.

The wingspan would be enough for 4 Merlins but could the wing structure be beefed up enough?
 
Justo Miranda said:
Albatross suffered stuctural failures ...
Click to expand...

Correction, structural failure singular, and the problem was corrected:
"During overload take-off tests with the second prototype E-3/GAEVW on August 27, 1938 the rear fuselage broke in two during the final stages of the third landing run. The aircraft reappeared within a few weeks as E-5 with reinforcement modifications said to have weighed but 12.5 lb. and these were embodied in five production aircraft which had been ordered for Imperial Airways Ltd."
- De Havilland Aircraft since 1909, A. J. Jackson, 2nd Edition 1978, Putnam & Co

Also the Albatross fuselage structure was built as a single shell and modification to a bomber would have required extensive redesign and major changes in construction technique to give the necessary opening for turrets and bomb bay.

Better to start from scratch.

Jon
 
PMN1 said:
4 Merlins vs 4 Gipsy engines should give quite a bit of extra power for beefing up the structure.

The wingspan would be enough for 4 Merlins but could the wing structure be beefed up enough?
Click to expand...

Engines are similar in size, the Merlin weighing from 320 ~ 400+ pounds more (for early marks, much more for later types) plus you'd have to factor in the weight of the liquid-cooling system for the Merlin.

Jon
 
Jemiba said:
The only one I can think of in the moment is the B-18, but I don't know, if there was more
than a superficial resemblance left with the DC2 in the end.
Click to expand...

Speaking in terms of structure and systems they were very similar, the outer wing panels were the same as was the empennage.

Jon
 
From "Back to the drawing board" by Bill Gunston , Airlife publishing Ltd. 1996
 

Attachments

  • Escanear0001.jpg
    Escanear0001.jpg
    21.7 KB · Views: 578
  • Escanear0002.jpg
    Escanear0002.jpg
    110 KB · Views: 579
Justo Miranda said:
From "Back to the drawing board" by Bill Gunston , Airlife publishing Ltd. 1996
Click to expand...

Not a matter of failure caused by structural design Justo, rather it was an issue of poor maintenance and the exigencies of wartime operations.

Jon
 
... de Havilland's and the Air Ministry continued to seriously consider a bomber variant
of the DH.91 Albatross.Aerodynamic cleanness and a minimun skin area would guarantee
high speed , and given an increased maximum take-off weight of 14.741kg it was calculated
the bomber version would cruise at 338km/h on only 1.280hp and carry up to 2,721kg bomb
load to Berlin at a fuel consumption of 2.5 airmiles per 4.54 litre.

In April 1938 further studies were made for an Albatross powered by two Rolls Royce Merlins.
Here was the starting point from which further private venture work by DH resulted in
the Mosquito...

so far :Ken Wixey in 'Albatross ,de Havilland's long-legged beauty'
Air Enhusiast 53 Spring 1994.

Maybe the two RR powered unbuilt variant was the intial DH.96 design?

(perhaps one of the artists on this forum can-possibly- produce
a sketch of the 'might have been ' Albatross bomber :)
 
lark said:
a sketch of the 'might have been ' Albatross bomber :)
Click to expand...

One, wildly speculative attempt:

http://www.secretprojects.co.uk/forum/index.php/topic,5582.0.html
 
Thanks Stephen,

It's a personal opinion ,but given the meagre info,the unarmed version is close
to the design as described...
 
From ‘RAF Bomber Command and its aircraft 1936-1940’ by James Goulding and Philip Moyes.

Powered by four de Havilland Gipsy Twelve Srs I engines of 525hp each, the Albatross could carry a 6,000lb payload over a range that would include Berlin and back, cruising at 210mph. With such as performance a military version of the aircraft seemed to have possibilities and a project was drafted which would conform to Specification P.13/36. This was projected with two Rolls-Royce Merlin engines, but this bomber was underpowered and not able to meet the specification requirements. With Merlins the top speed would have been 260mph and it could carry 4,000lb of bombs at 230mph for 1,500 miles. To meet the specification, double the power was needed, which was not surprising as all the other P.13/36 designs projected were mostly using two Vultures, with Sabres, Centaurus or Hercules as alternative power plants.

In August 1938 a revised twin-Merlin bomber was projected – again of similar size to the Albatross – but it too proved unsatisfactory.

Towards the end of 1938 de haviland proposed a different bomber layout, no longer an adaptation of the Albatross design but a smaller, three-seat twin-Merlin design with a top speed of 300mph and a cruising speed of 268mph. This design had fixed forward armament and manually operated guns. All-wood construction was again suggested.


Now given the Albatross had a 105ft wingspan, double the power should have been easy – four Merlins even if the wingspan was reduced to 100ft (was there a restriction on the P.13/36 wingspan?), but as i've said before, can the wing take it??

The P.13/36 was originally wanting the possibility of catapult launch and the ability to carry four later two torpedoes internally, what does that suggest for the strength and layout of this de Haviland design?

If faced with official disinterest, what would be de Haviland’s ability to make a racing aircraft (like the Comet) of the size, weight and shape as the actual Mosquito to prove their theory?
 
In the same chapter mention is also made of a bomber variant of the DH-95 Flamingo.
Is there anyone who ever have seen illustrations of this design.
Much searchwork in books and other publications about DeHavilland produced no results..
 
Somewhere in the old Air Enthusiast series there was a piece on using the Albatross as an inflight refuelling tanker; Flight Refuelling Ltd style......

Does any one know the article I mean?

Terry (Caravellarella)
 
That photo looks similar to several others showing Fw 200 Condors, another type, which
was (ab-)used as a make-shift bomber.
Click to expand...

You took the words right out of my mouth!

Regards
Pioneer
 
That drawing without doubt is a fake, taking "4-engined Mosquito" a little bit too literal. But I still have
enough faith in Tony Buttlers research, to believe, that such a derivative actually was studied by de Havilland.
 
Jemiba said:
That drawing without doubt is a fake, taking "4-engined Mosquito" a little bit too literal. But I still have
enough faith in Tony Buttlers research, to believe, that such a derivative actually was studied by de Havilland.
Click to expand...


May be Mr. Tony Buttler has more info my dear Jemiba,but of course that drawing is fake.
 
hesham said:
... but of course that drawing is fake.
Click to expand...

Careful, the question is, if it was made and published to pretend, that it is a true project, here
the four engined Mosquito, or better, the study for such an aircraft. If the drawing shall just show,
what it could have looked like, it's an attempt for a reconstruction, not realy a fake. So, principally
the same picture can be both: If you say "Here's an original drawing of the 4-engined Mossie !",
it is, if you say, "That's what it may have looked like", it's not ! Difficult theme, I know.
 
According to the people from the ww2aircraftnet , the planviewdrawing of
the 4-engined Mosquito found it origings
on a what if website.
There are several variants of this drawing on the ww2aicraftnet...
(thread - de Havilland 4 engined unarmed bomber)
 
Jemiba said:
Was there ever a succesful bomber design derived directly from a passenger aircraft ?
The only one I can think of in the moment is the B-18, but I don't know, if there was more
than a superficial resemblance left with the DC2 in the end.
Click to expand...


Depending on your definition of "bomber", the MR Nimrod could count - there's a lot of DH Comet in that airplane.


As for the colour image hesham provided, in the context of discussing what a four-engined Mosquito might have looked like, I think it's more than justified to leave it right here where it is, fake or otherwise.
 
lark said:
According to the people from the ww2aircraftnet , the planviewdrawing of
the 4-engined Mosquito found it origings
on a what if website. ...
Click to expand...

That what-if drawing was originally rendered by Secret Projects member Jon Carr Farrelly.
 
Stephen , I still wonder if Jon CF 's what iff plane is based on
original ,inside information.
In an Aeroplane Monhtly special about the Mosquito ,(Nov. year 2000 I think) a drawing
is shown of a proposed Mosquito variant with 4-gun tailturret (part drawing)
 
Wow, blast from da past. ;D

That was a super-quickie drawing, I did later mod the drawing by moving the outboard engines aft,
I'll have to dig around the ol' hard-drive and see if I still have it.

No inside info, pure speculation. :)
 

Similar threads

Please donate to support the forum.

Back
Top Bottom