ChuckAnderson
ACCESS: Confidential
- Joined
- 10 May 2006
- Messages
- 188
- Reaction score
- 36
Hi Everyone!
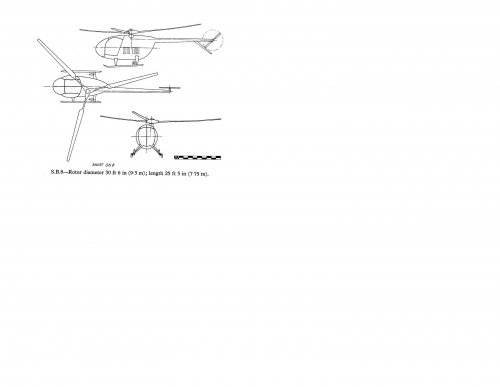
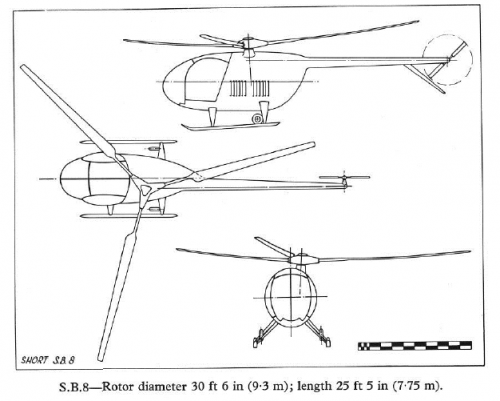
This design (the Shorts S.B.8), seems a little odd to me in one aspect, namely the single main rotor offset to one side, rather than being directly centered.
I've never seen that done with a single main rotor.
Are there any other helicopter designs that have the single main rotor offset?
Chuck
This design (the Shorts S.B.8), seems a little odd to me in one aspect, namely the single main rotor offset to one side, rather than being directly centered.
I've never seen that done with a single main rotor.
Are there any other helicopter designs that have the single main rotor offset?
Chuck