- Joined
- 26 May 2006
- Messages
- 33,049
- Reaction score
- 12,647
Hi,
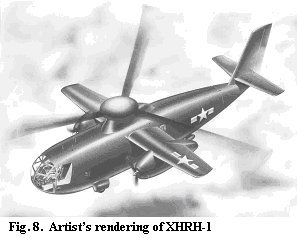
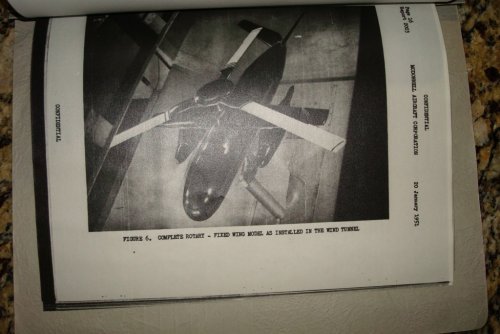
here is three McDonnell helicopter projects,the Model 78,86 and 113.
http://www.airandspacemuseum.org/MacsHelicopters.htm
here is three McDonnell helicopter projects,the Model 78,86 and 113.
http://www.airandspacemuseum.org/MacsHelicopters.htm