You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Bell projects
- Thread starter Justo Miranda
- Start date
- Joined
- 22 January 2006
- Messages
- 4,062
- Reaction score
- 1,581
Justo,
would you please post Model 2 picture? I'd love to see it.
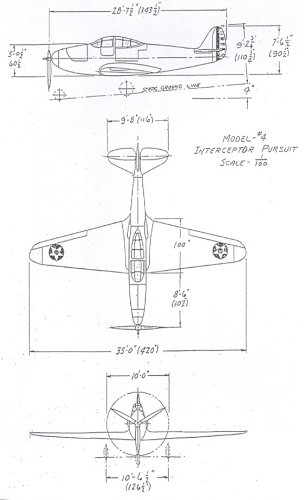
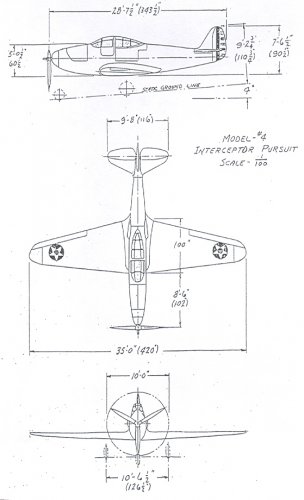
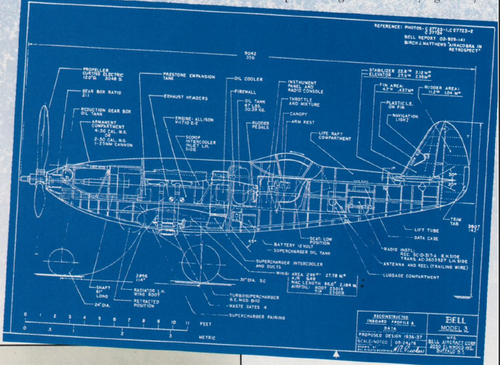
Model 3 and 4 were both fighter projects from 1937.Both were preliminary proposals submitted by Bell to Army Air Corps specification X-609 issued on March 1937 for a single- seat, single-engine (V-1710 with turbo-supercharger) high altitude interceptor.
It would have been a complementary type to the winner of X-608 (Lockheed P-38) for 1940-45 USAAC fighter force, according to US aislacionist policy from that years.
Armament for Model 3 consisted of a single 25 mm cannon and 2 0.50in machine guns (option for 2 more 0.50in MG) in forward fuselage. The engine was placed between the nose and the cockpit. It progressed to full-scale mock-up only because of poor visibility. It latter influencied the design of Model 32/XP-77
Tech Data: Span: 10,67 m, Lenght: 9,04 m, height: 3,61 m, Wing Area: 27,78 m2, Loaded weight: 2,446 Kg.
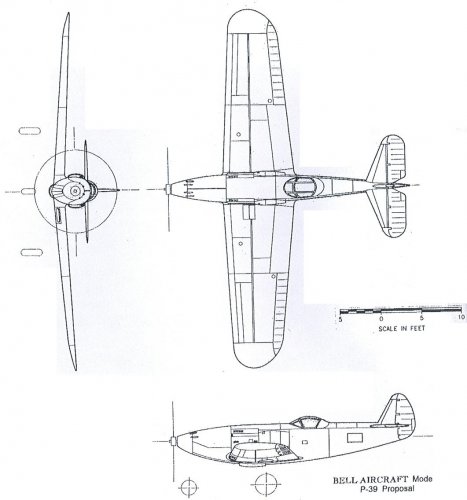
Model 4 reversed Model 3 cockpit/engine position. It was selected as winning design and further develoment resulted into Model 11 (XP-39) and Model 12 (YP-39).
Source: Bell Aircraft. A J Pelletier. Putnam
More info here:
http://www.secretprojects.co.uk/forum/index.php/topic,183.0.html
On post #82 you can see Apophenia's superb Model 3 render.
would you please post Model 2 picture? I'd love to see it.
Model 3 and 4 were both fighter projects from 1937.Both were preliminary proposals submitted by Bell to Army Air Corps specification X-609 issued on March 1937 for a single- seat, single-engine (V-1710 with turbo-supercharger) high altitude interceptor.
It would have been a complementary type to the winner of X-608 (Lockheed P-38) for 1940-45 USAAC fighter force, according to US aislacionist policy from that years.
Armament for Model 3 consisted of a single 25 mm cannon and 2 0.50in machine guns (option for 2 more 0.50in MG) in forward fuselage. The engine was placed between the nose and the cockpit. It progressed to full-scale mock-up only because of poor visibility. It latter influencied the design of Model 32/XP-77
Tech Data: Span: 10,67 m, Lenght: 9,04 m, height: 3,61 m, Wing Area: 27,78 m2, Loaded weight: 2,446 Kg.
Model 4 reversed Model 3 cockpit/engine position. It was selected as winning design and further develoment resulted into Model 11 (XP-39) and Model 12 (YP-39).
Source: Bell Aircraft. A J Pelletier. Putnam
More info here:
http://www.secretprojects.co.uk/forum/index.php/topic,183.0.html
On post #82 you can see Apophenia's superb Model 3 render.
Maveric said:Great find Justo,
but 2times the model 4? If you have, please post some technical data to all your posted projects.
Great thanks, Servus Maveric
Sorry
Here Model 2
Attachments
pometablava said:Justo,
would you please post Model 2 picture? I'd love to see it.
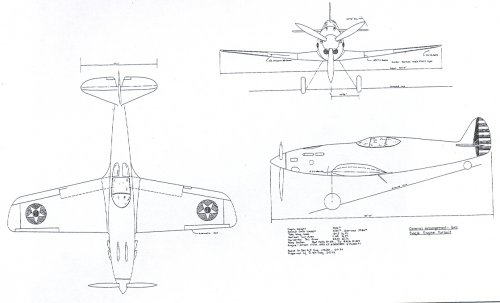
Sorry Please find attached Model 2 drawings and performances
Span 30 ft
lenght 25 ft-10 in.
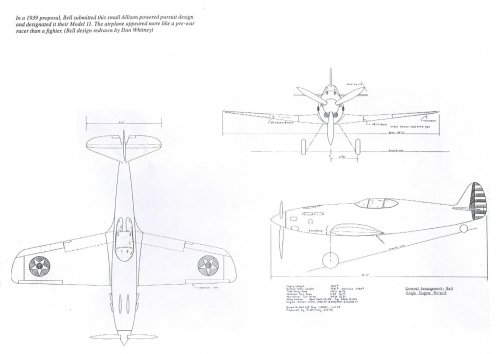
The Bell model 2 is in fact the model 11.
(maybe there's confusion with Roman figure II)
The design was smaller than the P-39.
It had a span of just 30ft ,four ft less than the Airacobra.
Fuselage lenght 28fr 10in.
Selected powerplant Allison V-1710-37 engine.
The model 11 was apparently in response to an Air Corps competition in 1939.
Bell's priiminary design wa completed during the middle of 1939
and may possibly have been an internal designs study in preparation
for the R40-C competition.
(maybe there's confusion with Roman figure II)
The design was smaller than the P-39.
It had a span of just 30ft ,four ft less than the Airacobra.
Fuselage lenght 28fr 10in.
Selected powerplant Allison V-1710-37 engine.
The model 11 was apparently in response to an Air Corps competition in 1939.
Bell's priiminary design wa completed during the middle of 1939
and may possibly have been an internal designs study in preparation
for the R40-C competition.
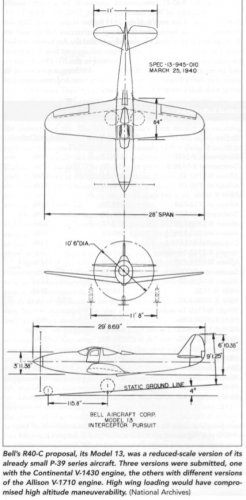
Maybe it had the looks but infact it
was a small-see dimensions- conventional pursuit design...
(project engineer was J.Trotter)
Woods was the project engineer for the models 13 ,13A and 13B.
proposals to R40-C
Source is the Bell Aircraft modelnumbers list.
was a small-see dimensions- conventional pursuit design...
(project engineer was J.Trotter)
Woods was the project engineer for the models 13 ,13A and 13B.
proposals to R40-C
Source is the Bell Aircraft modelnumbers list.
- Joined
- 22 January 2006
- Messages
- 4,062
- Reaction score
- 1,581
Maybe it had the looks but infact it
was a small-see dimensions- conventional pursuit design...
I agree with you. Please see that I talk about XP-47 (and also the XP-46) category not the XP-47B
lark said:The Bell model 2 is in fact the model 11.
(maybe there's confusion with Roman figure II)
The design was smaller than the P-39.
It had a span of just 30ft ,four ft less than the Airacobra.
Fuselage lenght 28fr 10in.
Selected powerplant Allison V-1710-37 engine.
The model 11 was apparently in response to an Air Corps competition in 1939.
Bell's priiminary design wa completed during the middle of 1939
and may possibly have been an internal designs study in preparation
for the R40-C competition.
You are right.You can see in this drawing that it is Model 11 , no Model II
Attachments
You're right of course Pome..
XP-47 and XP-47A were much smaller pursuit designs
like the model 11 in the the true late 30's fashion.
The info I put here was found in the indispensible " Cobra" - Schiffer
XP-47 and XP-47A were much smaller pursuit designs
like the model 11 in the the true late 30's fashion.
The info I put here was found in the indispensible " Cobra" - Schiffer
- Joined
- 8 March 2009
- Messages
- 1,009
- Reaction score
- 1,096
- Joined
- 8 March 2009
- Messages
- 1,009
- Reaction score
- 1,096
Model 18 trainer
From here; http://wnyaerospace.org/?p=2164
From here; http://wnyaerospace.org/?p=2164
Attachments
- Joined
- 26 May 2006
- Messages
- 33,402
- Reaction score
- 13,394
sienar said:Model 18 trainer
From here; http://wnyaerospace.org/?p=2164
Wow,nice find Sienar.
- Joined
- 25 June 2009
- Messages
- 14,040
- Reaction score
- 3,951
sienar said:Model 18 trainer
From here; http://wnyaerospace.org/?p=2164
Thanks for the beautiful photos, sienar.