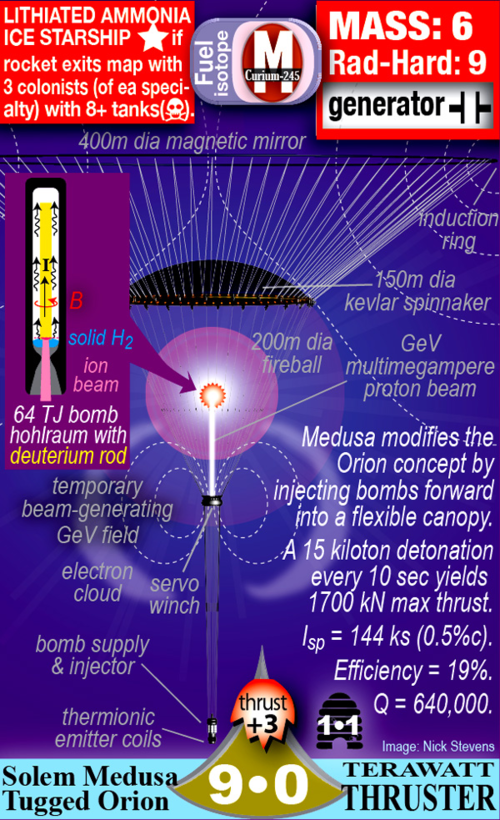
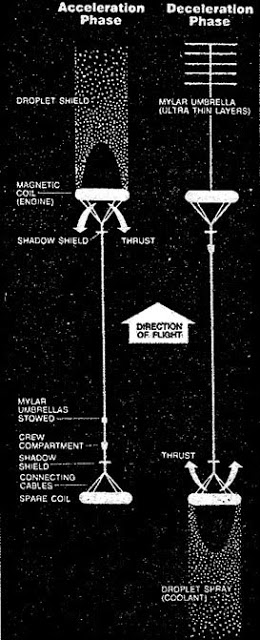
chimeric oncogene
ACCESS: Secret
- Joined
- 23 May 2019
- Messages
- 304
- Reaction score
- 295
While most proposals for Orion ground launches have included chemical first stages of some from, the most efficient way to launch an Orion appears to be from the ground. This is obviously impracticable under current political climates and cost-effectiveness calculi, but a man can dream...
A brief overview of the internet gives the suggestion that ground launches of Orion were envisaged to occur at the Nevada Test Site, possibly with a graphite-lined pad of some sort. Other options might have been the mid-Pacific: Johnston Island, where a permanent high-yield test site was planned (and where the Starfish Prime shots were launched) or Bikini Atoll/Eniwetok (high-yield nuclear test sites) Had the Soviets built Project Orion, one could envisage them launching from a new pad at the Cosmodrome, somewhere in Kazakhstan, or from Novaya Zemlya (the weather will screw with launch schedules).
The most obvious selection criteria for a launch site include low population, proximity to the ocean (maybe), high latitude (maybe), and good, predictable weather.
Little needs to be said about low population density along the launch track, except that Castle Bravo’s 15-megaton fallout plume was 500km long, and that Las Vegas is 100km from the Nevada Test Site (where low yield weapons similar to those used by Orion were tested). The exclusion zone should be similar in scale to Nevada, and the dispersion of fallout in the upper atmosphere and use of pad coatings should minimize fallout. Launch over unpopulated territory is still desirable to minimize eye injuries and minimize the hazards resulting from a launch failure (ditching a thousand pulse units into deep ocean for recovery is relatively simple, ditching into Arizona or detonating in-flight over Texas is more complex).
Given that Orion construction was envisaged as similar to shipbuilding (I'll believe it when I see it) and given the modern tendency to site large factories in populated areas, an oceanic or coastal launch site appears to have some advantages. At any rate, shipping a 5,000-to-50,000-tonne spacecraft (100-meter pusher plate) from Norfolk (or Korea, or Japan) to the launch site by some sort of ship lifter might be easier than moving the blasted thing cross-country by rail (or assembling it at the launch site). Johnston Atoll may be easier to get to from Norfolk than central Nevada.
Atomic Rockets claims that high-latitude high-inclination launches to avoid injecting material into the Earth's radiation belts are a good idea; while individual 0.5-30kt pulse units will certainly be smaller than the megaton-yield Starfish Prime shots, Orion envisaged using hundreds of pulse units to reach orbit. The total kilotonnage is comparable. HiVOLT and other electromagnetic tether systems have been suggested to clear the Van Allen belts, but I know not whether they would readily solve the problem.
Good weather and predictable winds are desirable for space launches, nuclear tests, and easy ground operations. The Aleutian Islands and Antarctic coasts may be a high-latitude launch site, but both have terrible weather (and the Aleutians are not outside the “will charge the Van Allens” zone, for some reason).
Some other suggestions on my part include:
A brief overview of the internet gives the suggestion that ground launches of Orion were envisaged to occur at the Nevada Test Site, possibly with a graphite-lined pad of some sort. Other options might have been the mid-Pacific: Johnston Island, where a permanent high-yield test site was planned (and where the Starfish Prime shots were launched) or Bikini Atoll/Eniwetok (high-yield nuclear test sites) Had the Soviets built Project Orion, one could envisage them launching from a new pad at the Cosmodrome, somewhere in Kazakhstan, or from Novaya Zemlya (the weather will screw with launch schedules).
The most obvious selection criteria for a launch site include low population, proximity to the ocean (maybe), high latitude (maybe), and good, predictable weather.
Little needs to be said about low population density along the launch track, except that Castle Bravo’s 15-megaton fallout plume was 500km long, and that Las Vegas is 100km from the Nevada Test Site (where low yield weapons similar to those used by Orion were tested). The exclusion zone should be similar in scale to Nevada, and the dispersion of fallout in the upper atmosphere and use of pad coatings should minimize fallout. Launch over unpopulated territory is still desirable to minimize eye injuries and minimize the hazards resulting from a launch failure (ditching a thousand pulse units into deep ocean for recovery is relatively simple, ditching into Arizona or detonating in-flight over Texas is more complex).
Given that Orion construction was envisaged as similar to shipbuilding (I'll believe it when I see it) and given the modern tendency to site large factories in populated areas, an oceanic or coastal launch site appears to have some advantages. At any rate, shipping a 5,000-to-50,000-tonne spacecraft (100-meter pusher plate) from Norfolk (or Korea, or Japan) to the launch site by some sort of ship lifter might be easier than moving the blasted thing cross-country by rail (or assembling it at the launch site). Johnston Atoll may be easier to get to from Norfolk than central Nevada.
Atomic Rockets claims that high-latitude high-inclination launches to avoid injecting material into the Earth's radiation belts are a good idea; while individual 0.5-30kt pulse units will certainly be smaller than the megaton-yield Starfish Prime shots, Orion envisaged using hundreds of pulse units to reach orbit. The total kilotonnage is comparable. HiVOLT and other electromagnetic tether systems have been suggested to clear the Van Allen belts, but I know not whether they would readily solve the problem.
Good weather and predictable winds are desirable for space launches, nuclear tests, and easy ground operations. The Aleutian Islands and Antarctic coasts may be a high-latitude launch site, but both have terrible weather (and the Aleutians are not outside the “will charge the Van Allens” zone, for some reason).
Some other suggestions on my part include:
- The Auckland Islands off the southern coast of New Zealand (weather and ease of access)
- The Falklands/South Georgia (weather)
- Hudson Bay (weather)
- the coast of Alaska (weather)
Last edited:
And yes due to the numerous issues of detonating multiple nuclear explosives low in the atmosphere/magnitosphere it is disirable to have an alternative means of getting such a vehicle into low Earth orbit, there is the conundrum due to it being actually vastly cheaper and easier to build such a vehicle on Earth and then launching it into orbit. And it's not like people have forgotten about the idea either 
