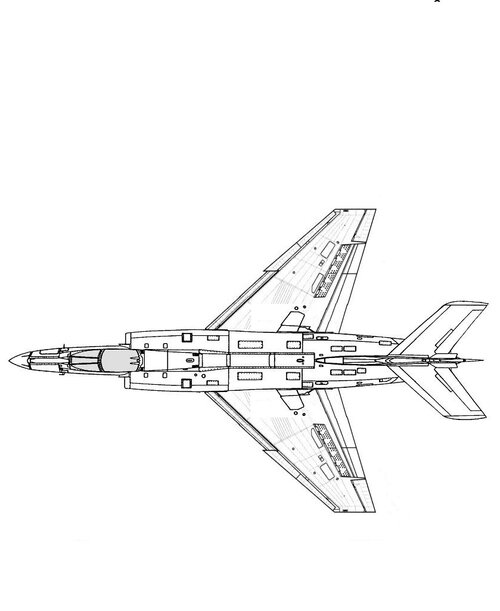
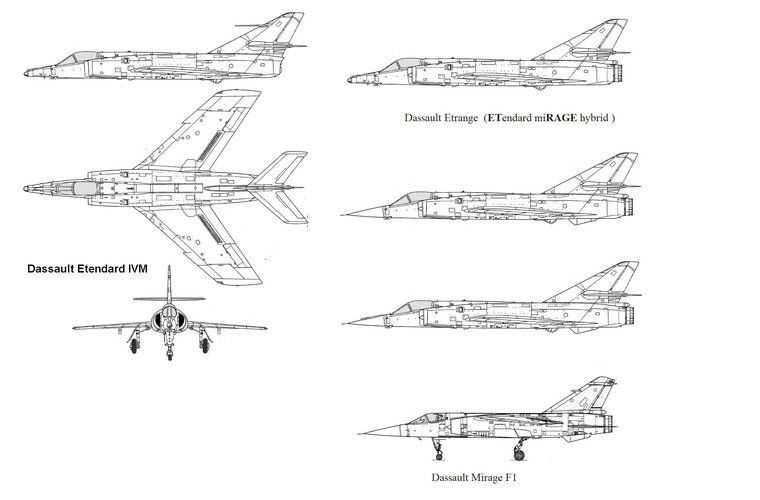
In the mid-1950s the French were developing 2 Dassault fighters in parallel: a high altitude supersonic interceptor (the Mirage delta), and a low altitude light tactical fighter (the Mystère/Etendard series).
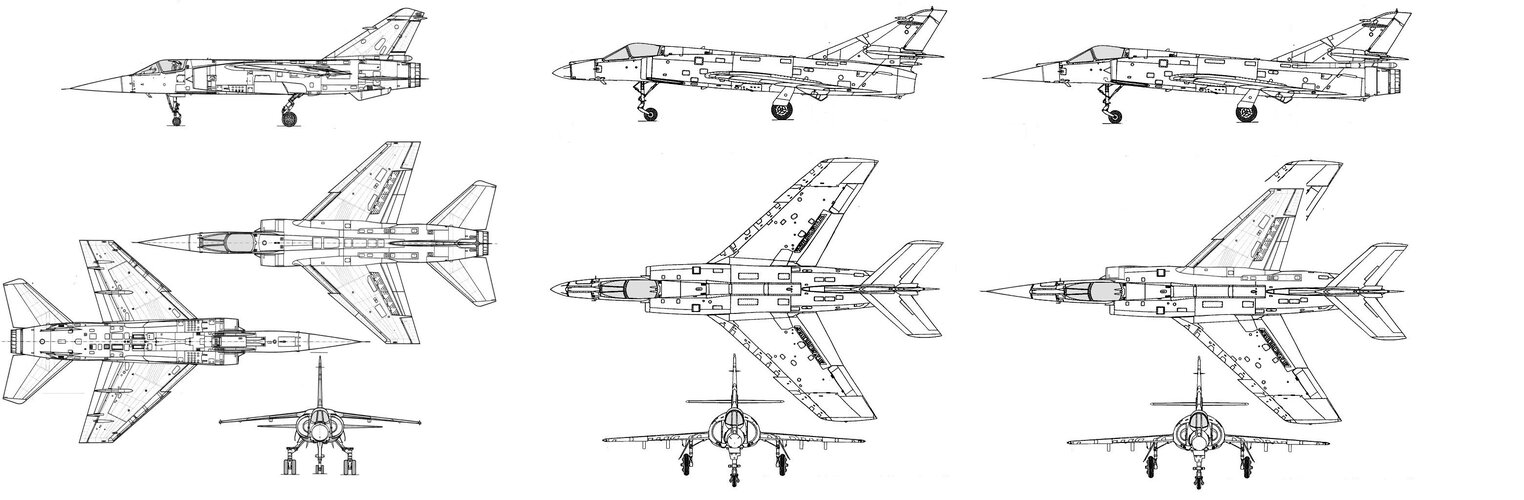
In hindsight the Mirage was a success while the Etendard was a mixed bag (not enough thrust and payload). This led to strange decisions in the 1960s, like buying Crusaders to fill the Aeronavale’s supersonic fighter gap, and buying Mirage IIIEs, IIIRs and Vs for low altitude strike/reconnaissance.
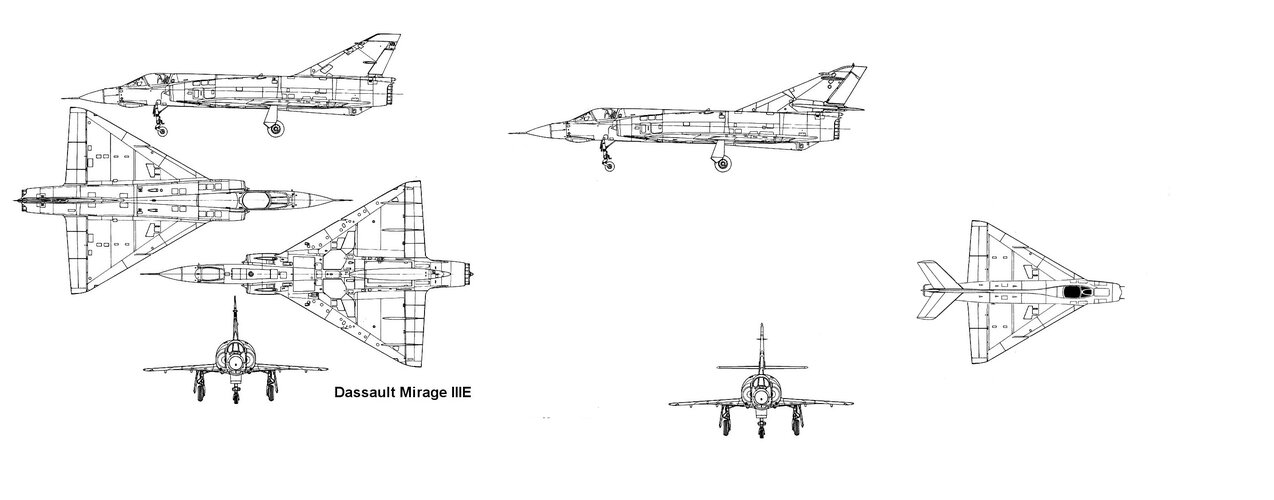
What if the French, with a little foresight, had decided to tweak the Etendard IV design with an afterburning Atar 9B, the same engine that made the Mirage III so successful?
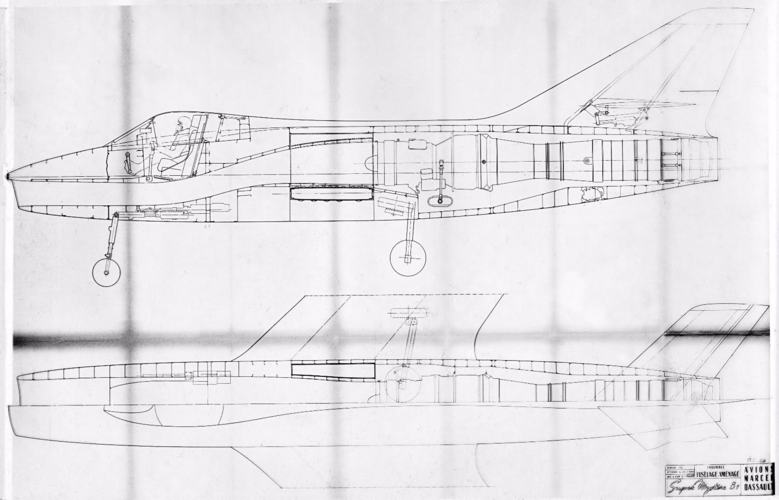
I could see this happening around summer 1957. The Mirage III and Etendard IV prototypes first flew in 1956, and it was soon clear that they were both great designs. The French were ready to order the first pre-production aircraft, which they quickly did by mid-1957. At the same time, Dassault was asked to build a test bed for the Atar 9 engine, the Super Mystère B4. So what if Dassault had ditched the SMB4 and suggested using the Etendard IV as the Atar 9 test bed instead, with the French Navy’s full support?
(As by now the performance of the Mirage III and F8U Crusader / F11F-1F Super Tiger must have been leaving them a little envious and worried about the little Etendard IV, while the SMB4 was an evolutionary dead end for Dassault!)
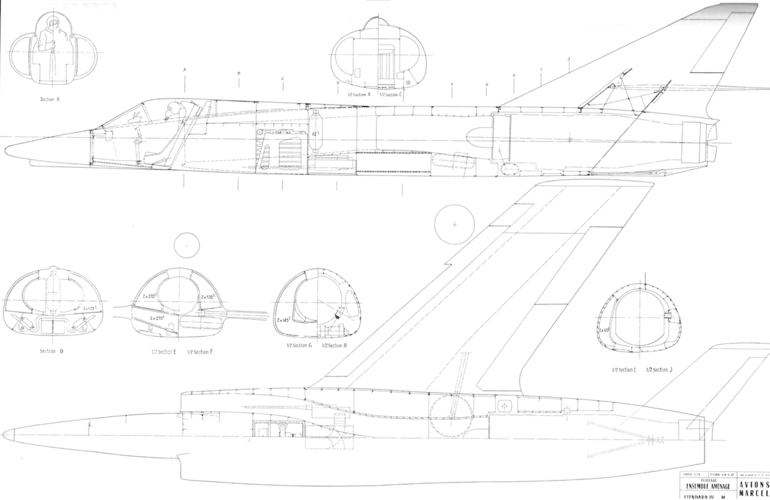
How realistic would it have been for Dassault to mash up the wing & front fuselage of an Etendard IV with the engine & rear fuselage of a Super Mystere B.4?
(This would have been an alternative to the BR.1120 Sirocco - see this thread: https://www.secretprojects.co.uk/th...-2-2-naval-fighter-proposal-from-1956-57.142/)
In hindsight the Mirage was a success while the Etendard was a mixed bag (not enough thrust and payload). This led to strange decisions in the 1960s, like buying Crusaders to fill the Aeronavale’s supersonic fighter gap, and buying Mirage IIIEs, IIIRs and Vs for low altitude strike/reconnaissance.
What if the French, with a little foresight, had decided to tweak the Etendard IV design with an afterburning Atar 9B, the same engine that made the Mirage III so successful?
I could see this happening around summer 1957. The Mirage III and Etendard IV prototypes first flew in 1956, and it was soon clear that they were both great designs. The French were ready to order the first pre-production aircraft, which they quickly did by mid-1957. At the same time, Dassault was asked to build a test bed for the Atar 9 engine, the Super Mystère B4. So what if Dassault had ditched the SMB4 and suggested using the Etendard IV as the Atar 9 test bed instead, with the French Navy’s full support?
(As by now the performance of the Mirage III and F8U Crusader / F11F-1F Super Tiger must have been leaving them a little envious and worried about the little Etendard IV, while the SMB4 was an evolutionary dead end for Dassault!)
How realistic would it have been for Dassault to mash up the wing & front fuselage of an Etendard IV with the engine & rear fuselage of a Super Mystere B.4?
(This would have been an alternative to the BR.1120 Sirocco - see this thread: https://www.secretprojects.co.uk/th...-2-2-naval-fighter-proposal-from-1956-57.142/)
Attachments
Last edited: