Most times when the XB-31 is covered, it's mentioned that the original design was a bomber version of the DC-4, yet the most popular drawing shown as the "XB-31" is the huge design with a 200 ft span, 4 R-3350s w/huge 3 blade props, an empennage similar to the A-26 in design & the long, slender fuselage with thetwin bubble canopies, like the XB-42 & -43 & C-74. Anyone ever see a drawing of the DC-4 version?
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Douglas XB-31
- Thread starter frank
- Start date
In Boeing B-29 Superfortress by Steve Page - Crowood
the Douglas XB-31 is labelled as the Douglas Model D-332F
to Requirement R-40-B of February 1940.
Not a single mention is made about the D.C.4 as the basis for
the XB-31. Nor do "McDonnell Douglas Aircraft since 1920"
by René j.Francillon-Putnam.
Could it be that the link between the DC-4 and the XB-31
goes back to "U.S Bombers B-1 to B-70" LLoyd S.Jones-Aero Publ.1966.This is the only source I ever saw this relation mentioned.
the Douglas XB-31 is labelled as the Douglas Model D-332F
to Requirement R-40-B of February 1940.
Not a single mention is made about the D.C.4 as the basis for
the XB-31. Nor do "McDonnell Douglas Aircraft since 1920"
by René j.Francillon-Putnam.
Could it be that the link between the DC-4 and the XB-31
goes back to "U.S Bombers B-1 to B-70" LLoyd S.Jones-Aero Publ.1966.This is the only source I ever saw this relation mentioned.
- Joined
- 8 January 2006
- Messages
- 1,605
- Reaction score
- 677
It could be interesting, in a way, since the original and aborted DC-4E program (inspired by the Lockheed "Excalibur" (later "Constellation") program) led to the Japanese G5N1. And the Japanese "learning experiences" with that design led to the G8N1.
Steve Pace
Aviation History Writer
- Joined
- 6 January 2013
- Messages
- 2,266
- Reaction score
- 167
It's Steve Pace; not Steve Page.
archipeppe
ACCESS: Top Secret
- Joined
- 18 October 2007
- Messages
- 2,291
- Reaction score
- 2,338
Steve Pace
Aviation History Writer
- Joined
- 6 January 2013
- Messages
- 2,266
- Reaction score
- 167
Very nice!
archipeppe
ACCESS: Top Secret
- Joined
- 18 October 2007
- Messages
- 2,291
- Reaction score
- 2,338
Steve Pace
Aviation History Writer
- Joined
- 6 January 2013
- Messages
- 2,266
- Reaction score
- 167
What else have you produced?
Email directly if you wish.
Email directly if you wish.
archipeppe
ACCESS: Top Secret
- Joined
- 18 October 2007
- Messages
- 2,291
- Reaction score
- 2,338
XB-70 Guy said:What else have you produced?
Email directly if you wish.
A lot of things, especially in astronautics.
In aeronautics a bunch of drawings (more or less 30) ranging from Airbus A 300 ZeroG to Northrop F 20.
If you have specific request you can address me directly at:
archipeppe@alice.it
Steve Pace
Aviation History Writer
- Joined
- 6 January 2013
- Messages
- 2,266
- Reaction score
- 167
It is 423
Jos Heyman
ACCESS: Top Secret
- Joined
- 15 February 2007
- Messages
- 597
- Reaction score
- 57
Lloyd Jones in his classic book on US bombers clearly states that the XB-31 was a a design study that covered various engineering studies. The model 423 was one of these but the design did not go beyond the study catagory. The picture that we see (and which is an orginal Jones picture) must therefore be considered as one of many designs.
- Joined
- 25 June 2009
- Messages
- 13,776
- Reaction score
- 3,046
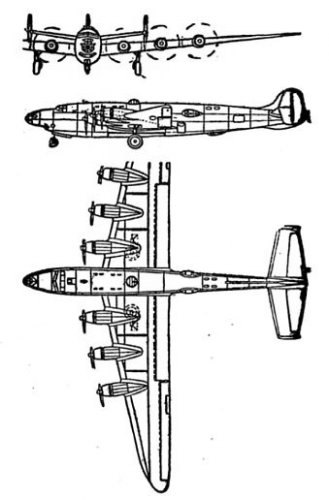
archipeppe said:My personal contribution about the matter.
Wow! The artwork is brilliant but I think the "Model 433" caption is a typo, should be Model 423 I think...
archipeppe
ACCESS: Top Secret
- Joined
- 18 October 2007
- Messages
- 2,291
- Reaction score
- 2,338
Stargazer2006 said:Wow! The artwork is brilliant but I think the "Model 433" caption is a typo, should be Model 423 I think...
Yep, you're right Stargazer it was my fault, the correct number is Douglas Model 423.
Anyway, I'm glad that you appreciated my work!!
Sentinel Chicken
American 71 Heavy, contact departure 126.47
I did this print back in 2006:

Close up of the nose:

Engine details:


Close up of the nose:

Engine details:

Steve Pace
Aviation History Writer
- Joined
- 6 January 2013
- Messages
- 2,266
- Reaction score
- 167
Beautiful!
archipeppe
ACCESS: Top Secret
- Joined
- 18 October 2007
- Messages
- 2,291
- Reaction score
- 2,338
Great drawing (just as usual) JP!!!!!!!
Sentinel Chicken
American 71 Heavy, contact departure 126.47
I still have quite a few of these prints, if anyone's interested, let me know, they're 16 x 20 inches in size.
Steve Pace
Aviation History Writer
- Joined
- 6 January 2013
- Messages
- 2,266
- Reaction score
- 167
How much $?
Sentinel Chicken
American 71 Heavy, contact departure 126.47
Sent you a forum PM.
I'm interested as well. Thanks.
Sentinel Chicken said:I still have quite a few of these prints, if anyone's interested, let me know, they're 16 x 20 inches in size.
- Joined
- 25 June 2009
- Messages
- 13,776
- Reaction score
- 3,046
frank said:Most times when the XB-31 is covered, it's mentioned that the original design was a bomber version of the DC-4, yet the most popular drawing shown as the "XB-31" is the huge design with a 200 ft span, 4 R-3350s w/huge 3 blade props, an empennage similar to the A-26 in design & the long, slender fuselage with thetwin bubble canopies, like the XB-42 & -43 & C-74. Anyone ever see a drawing of the DC-4 version?
Could it be this?
Attachments
- Joined
- 2 January 2011
- Messages
- 334
- Reaction score
- 308
While I do not yet have a lot of documentation on the XB-31, it is possible that the idea got its start with the "100 ton bomber".
The "bug-eye" version was, I believe, Model 423H, indicating that there were a bunch of design studies that preceeded it - possibly including the 100 tonner.
AlanG
The "bug-eye" version was, I believe, Model 423H, indicating that there were a bunch of design studies that preceeded it - possibly including the 100 tonner.
AlanG
- Joined
- 22 January 2006
- Messages
- 3,895
- Reaction score
- 1,160
Probably the 100 ton was already an early Model 423 iteration.
After the first "Super Bomber" competition, both Boeing and Douglas returned to the drawing board. Boeing started studies with Model 316 while Douglas produced a series of designs based in the DC-4. The lineage from Model 316 to Model 345 has been fully preserved. But we only have the 100 ton and the Model 423H from Douglas.
:-(
After the first "Super Bomber" competition, both Boeing and Douglas returned to the drawing board. Boeing started studies with Model 316 while Douglas produced a series of designs based in the DC-4. The lineage from Model 316 to Model 345 has been fully preserved. But we only have the 100 ton and the Model 423H from Douglas.
:-(
- Joined
- 25 June 2009
- Messages
- 13,776
- Reaction score
- 3,046
famvburg said:Based on the DC-4 or DC-4E?
The DC-4E of course. But please keep in mind that until it was rechristened as such when "our" DC-4 appeared, it was called just that, the "DC-4"...
- Joined
- 25 June 2009
- Messages
- 13,776
- Reaction score
- 3,046
famvburg said:Are you sure? All I ever saw regarding that design was DC-4E, "E" being for experimental.
Positive! All it takes is to look at period magazines and you'll see it's called the DC-4 all over.
- Joined
- 25 June 2009
- Messages
- 13,776
- Reaction score
- 3,046
famvburg said:Hmm. I've never looked thru any period mags that had the DC-4E in them.
Here is an excerpt from Skyways #88:
Attachments
- Joined
- 25 June 2009
- Messages
- 13,776
- Reaction score
- 3,046
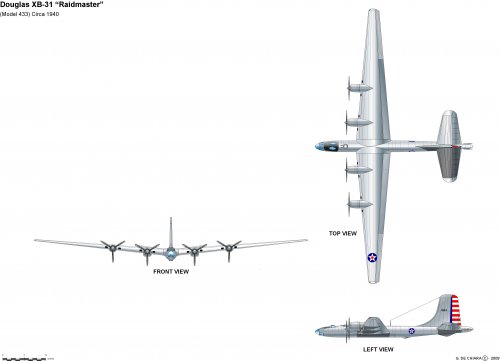
pometablava said:Is the "Raidmaster" nickname confirmed?
I don't think so. Until I see a Douglas or AF document quoting the name (even as a proposal) I'll consider it as a marketing trick by the model makers, just like the X-2 Starbuster or the XF-90 SuperStar!
Jos Heyman
ACCESS: Top Secret
- Joined
- 15 February 2007
- Messages
- 597
- Reaction score
- 57
Totally agree with Stargazer. The worst thing that we could do is 'create' history like the model makers do. And we should not give our support to the modelmakers.
- Joined
- 2 January 2011
- Messages
- 334
- Reaction score
- 308
The REAL XB-31
While I had thought to wait until the book for which I did this research is finished, I decided that perhaps now would be a good time to share a tiny portion of what I've found from ORIGINAL Douglas and USAAC documents and clarify the record.
As you will see from what follows, the XB-31 information that has been widely disseminated falls into the category of "repetition of the same old mistakes due to a lack of original research". Sadly, a large percentage of books on aircraft have been and are written by authors "gathering" information from other, already-incorrect books, not from doing original research.
While not wanting to repeat the correct parts of the record that are already out there I shall do so anyway with some extra tidbits thrown in along the way - but with "meat" saved for the book. I also do this because this website is filled with wonderful information from numerous researchers around the world who are generously willing to tell not only what they have but where and how they got it. We all spend lots of time and money coming up with this information, so those who are willing to share freely (not including the ones who won't tell you how they found what they found) are quite special. The primary source for the following is from Record Group 342 (RG342), also called the Sarah Clark Collection, at NARA II. RG342 is fairly easy to research as it has been catalogued and put into the computer. The sources for the drawings are the Douglas Archives as well as NARA II.
In January, 1940, the Air Corps released Type Specification XC-218 under Request For Data R40-B for a long-range 4-engine bomber with the following characteristics:
• High Speed (military rated power) at 25,000 feet altitude: 450mph max 300mph min
• Service Ceiling: 40,000ft max 30,000ft min
• Range: Not less than 5333 miles at 25,000ft with normal useful load at a speed not less than 200mph
• Normal (design useful load) carried internally was 2000lbs. Maximum alternate bomb load, in lieu of fuel, was 8000lbs. The capability of externally carrying
bombs up to 2000lbs in weight at reduced ranges was to receive consideration as long as the fixed equipment in the wing with no bomb attached did not
adversely effect performance.
• Crew, defensive armament, etc. were to be determined by the manufacturer and subsequently analyzed by Material Command.
Four manufacturers responded:
• Boeing submitted Model 341;
• Consolidated submitted Model LB-25;
• Douglas Model 332, the first of what would be seven versions (with numerous alternates within);
• Lockheed Model 51-58-01 and 04
In March, 1940 new Type Specifications XC-218 A were published, the previous specifications and submissions being deemed insufficient based on reports coming out the war in Europe, the potential for the U.S. to be in a war in both Europe and the Pacific and rapid technological change.
The new submissions from the manufacturers were:
Boeing Model 345 designation XB-29
Lockheed Model 51 designation XB-30
Douglas Model 332 designation XB-31
Consolidated Model 33 and 33A designation XB-32
All submissions used the R-3350 engine in at least one of the versions submitted for analysis.
As stated earlier, Douglas' Model 332 would eventually see seven different versions with numerous alternate versions within each, including different engines, single and multiple tails, etc. It would be the Model 332F that was considered most seriously and that would receive the XB-31 designation.
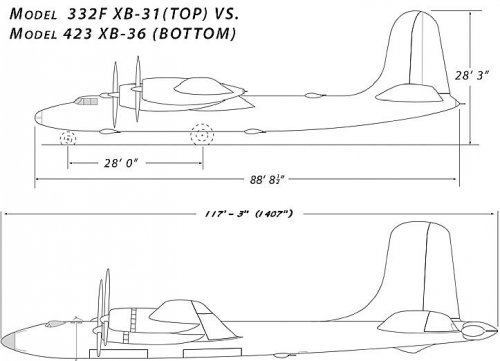
Below is a side view showing the Model 332F vs the Model 423. The drawings are to the same scale. As you can see, there is a substantial difference between the two. In addition, the Model 332F had a wingspan of 140ft 8.5" where the 423 had one of 207ft. The 332F was powered by the R-3350 Duplex Cyclone vs the Model 423's R-4360 Wasp Major, the engine of choice for the entries that would eventually yield the XB-36.
Though I have not yet come upon documentation to prove it, I believe the circumstantial evidence points to the Model 423 being Douglas' submission for "XB-36" project. At the very least, it was not the XB-31.
AlanG
While I had thought to wait until the book for which I did this research is finished, I decided that perhaps now would be a good time to share a tiny portion of what I've found from ORIGINAL Douglas and USAAC documents and clarify the record.
As you will see from what follows, the XB-31 information that has been widely disseminated falls into the category of "repetition of the same old mistakes due to a lack of original research". Sadly, a large percentage of books on aircraft have been and are written by authors "gathering" information from other, already-incorrect books, not from doing original research.
While not wanting to repeat the correct parts of the record that are already out there I shall do so anyway with some extra tidbits thrown in along the way - but with "meat" saved for the book. I also do this because this website is filled with wonderful information from numerous researchers around the world who are generously willing to tell not only what they have but where and how they got it. We all spend lots of time and money coming up with this information, so those who are willing to share freely (not including the ones who won't tell you how they found what they found) are quite special. The primary source for the following is from Record Group 342 (RG342), also called the Sarah Clark Collection, at NARA II. RG342 is fairly easy to research as it has been catalogued and put into the computer. The sources for the drawings are the Douglas Archives as well as NARA II.
In January, 1940, the Air Corps released Type Specification XC-218 under Request For Data R40-B for a long-range 4-engine bomber with the following characteristics:
• High Speed (military rated power) at 25,000 feet altitude: 450mph max 300mph min
• Service Ceiling: 40,000ft max 30,000ft min
• Range: Not less than 5333 miles at 25,000ft with normal useful load at a speed not less than 200mph
• Normal (design useful load) carried internally was 2000lbs. Maximum alternate bomb load, in lieu of fuel, was 8000lbs. The capability of externally carrying
bombs up to 2000lbs in weight at reduced ranges was to receive consideration as long as the fixed equipment in the wing with no bomb attached did not
adversely effect performance.
• Crew, defensive armament, etc. were to be determined by the manufacturer and subsequently analyzed by Material Command.
Four manufacturers responded:
• Boeing submitted Model 341;
• Consolidated submitted Model LB-25;
• Douglas Model 332, the first of what would be seven versions (with numerous alternates within);
• Lockheed Model 51-58-01 and 04
In March, 1940 new Type Specifications XC-218 A were published, the previous specifications and submissions being deemed insufficient based on reports coming out the war in Europe, the potential for the U.S. to be in a war in both Europe and the Pacific and rapid technological change.
The new submissions from the manufacturers were:
Boeing Model 345 designation XB-29
Lockheed Model 51 designation XB-30
Douglas Model 332 designation XB-31
Consolidated Model 33 and 33A designation XB-32
All submissions used the R-3350 engine in at least one of the versions submitted for analysis.
As stated earlier, Douglas' Model 332 would eventually see seven different versions with numerous alternate versions within each, including different engines, single and multiple tails, etc. It would be the Model 332F that was considered most seriously and that would receive the XB-31 designation.
Below is a side view showing the Model 332F vs the Model 423. The drawings are to the same scale. As you can see, there is a substantial difference between the two. In addition, the Model 332F had a wingspan of 140ft 8.5" where the 423 had one of 207ft. The 332F was powered by the R-3350 Duplex Cyclone vs the Model 423's R-4360 Wasp Major, the engine of choice for the entries that would eventually yield the XB-36.
Though I have not yet come upon documentation to prove it, I believe the circumstantial evidence points to the Model 423 being Douglas' submission for "XB-36" project. At the very least, it was not the XB-31.
AlanG
Attachments
Similar threads
-
Douglas 4-engine pre-war long-range bombers
- Started by ACResearcher
- Replies: 2
-
-
Martin XB-16 and XB-16A bomber projects (Model 145)
- Started by Stargazer
- Replies: 64
-
-
Douglas ATA-A1: Another « Skybus » project !
- Started by Stargazer
- Replies: 18




![Douglas_XB-31_model[1].jpg](/data/attachments/69/69436-5de5ad5684fb57595b74ebef64ee84a1.jpg)