Vympel plans to develop air-to-air missiles for Russia's PAK FA fighter
19-May-2006 Jane’s Missiles and Rockets
Russia's Vympel (Toropov) State Engineering Design Bureau Joint Stock Company (JSC) is developing advanced air-to-air missiles of short, medium and long range for use on the planned fifth-generation fighter (PAK FA), writes Yevgeniy Letunovsky. According to Vympel chief designer Gennady Sokolovsky, the new missiles are being designed for carriage within an internal weapons bay. Stowing the missiles in an internal bay helps to reduce a fighter's radar cross-section (RCS). The F-22 and F-35 incorporate weapons bays, and the PAK FA will be the first Russian fighter with this feature.
Sokolovsky said that the new missiles will incorporate advanced concepts in areas such as configuration, propulsion, guidance and warhead technology, and are intended to allow the PAK FA to win air superiority over Western aircraft such as the Lockheed Martin F-22 and F-35, and the Eurofighter Typhoon.
Under a reorganisation of the Vympel design bureau, Gennady Sokolovsky (who formerly had the dual role of both General Designer and General Director) now serves as General Designer. The General Director of the Vympel is Victor Rats, while Peter Vasilev is chief of the design department.
Another goal of the programme is to create missiles of all-Russian manufacture. Many current air-to-air missiles carried by Russian aircraft incorporate subsystems provided by manufacturers in countries such as Ukraine. For example, both current versions of the R-73 - the R-73K (fitted with the Krechet radar proximity fuze) and the R-73L (with the Yantar laser proximity fuze) - are based on the Mayak-80 series of infrared (IR) seekers produced by the Arsenal State Kiev Enterprise in Ukraine, an autopilot produced by the Moscow-based AVIONIKA MNPK, and the RDTT-295 solid-propellant rocket motor developed by the ISKRA State Unitary Enterprise in Moscow.
For many years following the break-up of the former Soviet Union, political factors slowed work on creating improved R-73 variants. However, two interim models were produced - the K-74 (probably begun as izdeliye 740), with an improved Mayak-80M IR seeker operating at angles of +/-60ⅹ off boresight, and the K-74M (izdeliye 750) with an angle of +/-75ⅹ.
For the PAK FA, Vympel is developing two new missiles based on R-73/R-74 technology. The first of these is izdeliye 760. Based on the K-74M, this is intended to match the performance of the MBDA Advanced Short-Range Air-to-Air Missile (ASRAAM) and the Raytheon AIM-9X Sidewinder. It will have an improved IR seeker, an inertial control system, a datalink receiver for target updates and an advanced rocket motor with a longer burn time. To make the missile suitable for internal carriage, its cross-section will be reduced to 320x320 mm.
To maximise the weapon's coverage, it can be fired in lock-on-after-launch (LOAL) mode, starting under inertial control before achieving in-flight lock-on. It will be able to engage targets up to 160ⅹ from the aircraft's heading.
According to a Vympel representative, izdeliye 760 is about to begin flight tests. Development is due to be completed in 2010.
The follow-on K-MD (izdeliye 300) is intended to outperform the ASRAAM and AIM-9X. Although it will draw on the experience gained with the R-73/R-74 series, for most practical purposes it will be an all-new missile.
Its guidance system will be based on a new IR seeker incorporating a focal-plane array (FPA). This will have more than twice the lock-on range of the izdeliye 760 seeker, a high resistance to countermeasures and a target-recognition capability.
Russian air-to-air missile programmes have been slow to adopt FPA technology, which is already used in 'dogfight' missiles such as the AIM-9X, ASRAAM, the Diehl BGT Defence IRIS-T and Rafael's Python-4 and Python-5. Russian work in this field is still at an early stage.
The reason for this time lag is essentially historical - until now, the IR seekers for the R-73/74 series and other Russian short-range air-to-air missiles were developed by Arsenal in Kiev.
According to Peter Vasilev, chief of the Vympel design department, several Russian companies are candidates for the task of creating a state-of-the-art FPA-based seeker. Obvious candidates are the Geophizika JSC or GNPP Impulse companies, but the Azovskii Optiko-Mekhanicheskii Zavod (AOMZ) recently announced that it planned to work on advanced seeker technology.
Geophizika was responsible for the 36T IR seeker for the R-27T air-to-air missile, and for semi-active laser seekers such as the 24N1 used on the KH-29L and KH-25L air-to-surface missiles, and the 27N for KAB-500L and-1500L laser-guided bombs, while AOMZ manufactured all three. GNPP Impulse (formerly known as NII-504) has developed various types of semi-active laser and TV seekers.
The new missile will have an improved aerodynamic configuration of minimal drag, and will be powered by a dual-mode solid-rocket engine with a high specific impulse and a total burn time of about 100 seconds. The R-73 used a system of four moving thrust-vector control vanes mounted around the motor nozzle. For the K-MD, Vympel has developed what it described as 'a three-channel gas-dynamic control unit (gas control vanes)'. An adaptive warhead will provide optimised lethal effects to suit the final interception conditions.
Development of the K-MD is expected to end in 2013, giving the PAK FA a 'dogfight' weapon of much-increased range, all-round coverage and the ability to engage aircraft or missile targets.
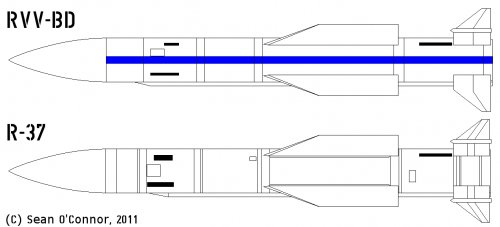
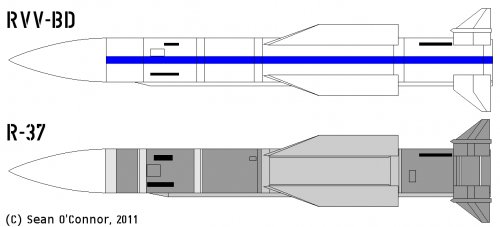
To provide the aircraft with a medium-range and long-range armament, new missiles will be developed based on the current R-77 and R-73 respectively. As with the short-range weapon, this will be an evolutionary process, starting with improved variants and moving towards what will eventually become an all-new missile.
The use of internal carriage for all three classes of missile, and for the aircraft's air-to-surface weapons, will require the use of a new pattern of launcher able to catapult the round out of the aircraft's weapons bay. Two versions are planned. The UVKU-50L lightweight launcher is intended to carry missiles weighing up to 300 kg. Heavier weapons weighing up to 700 kg will be carried on the UVKU-50U universal launcher.