[user-BG]
ACCESS: Restricted
- Joined
- 5 February 2024
- Messages
- 16
- Reaction score
- 26
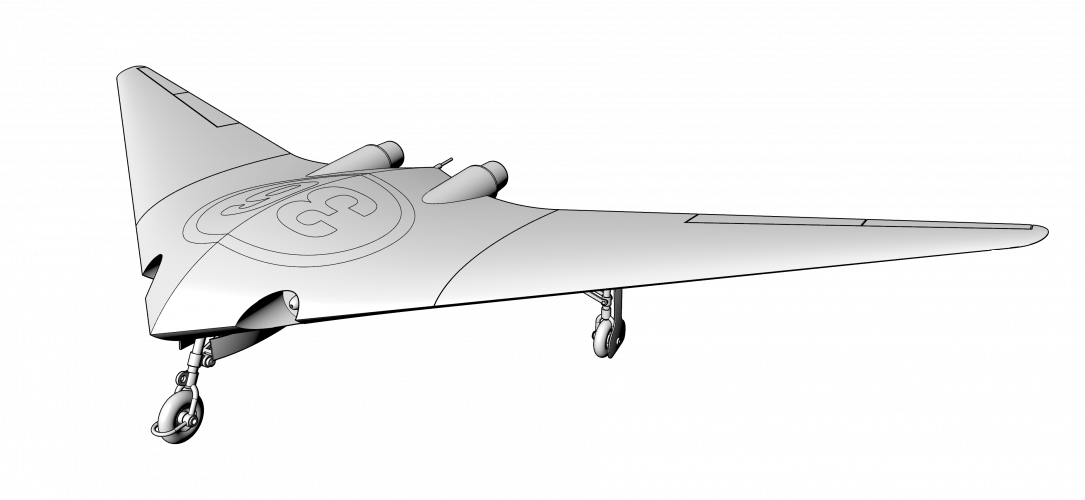
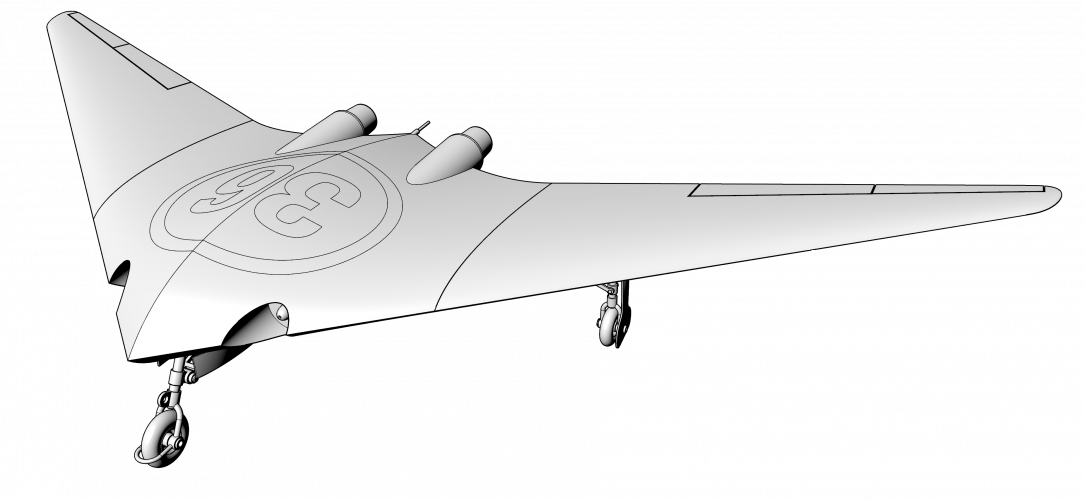
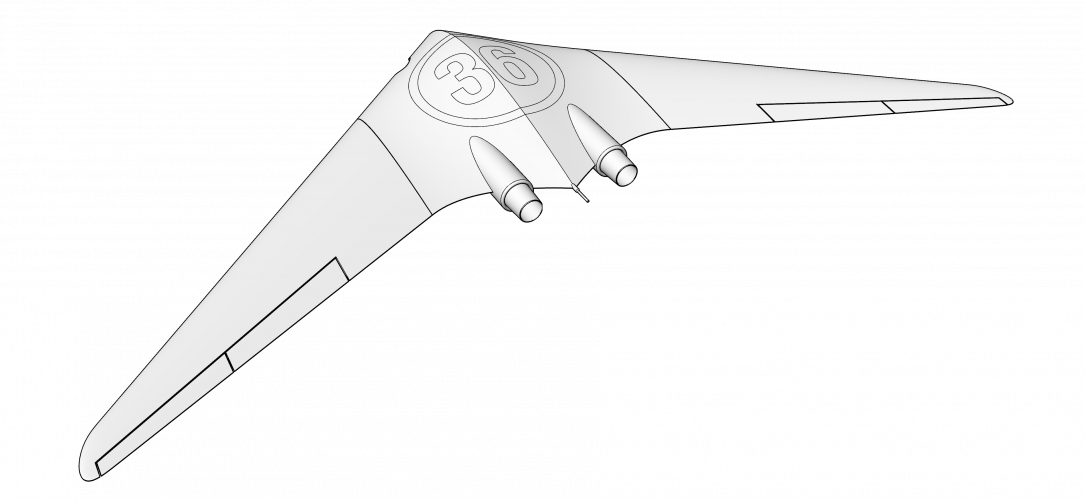
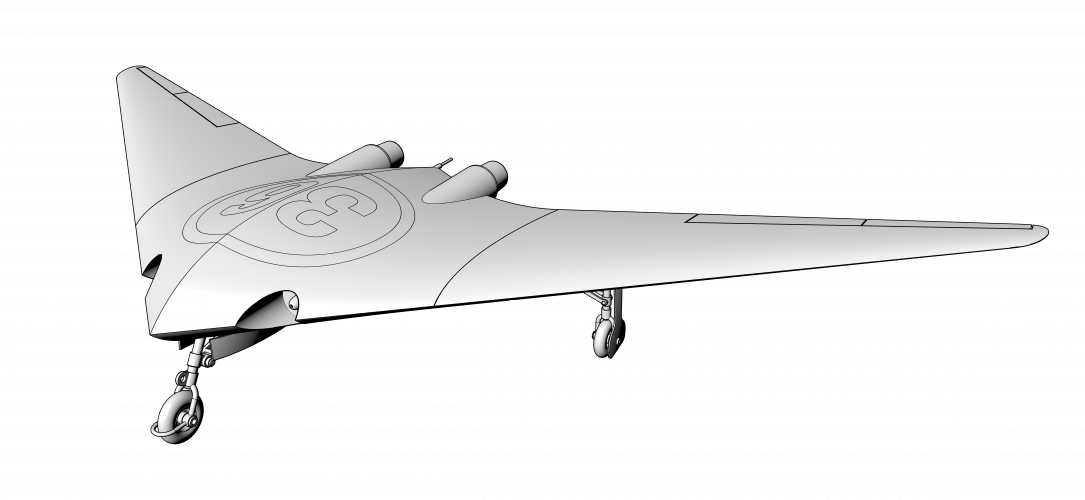
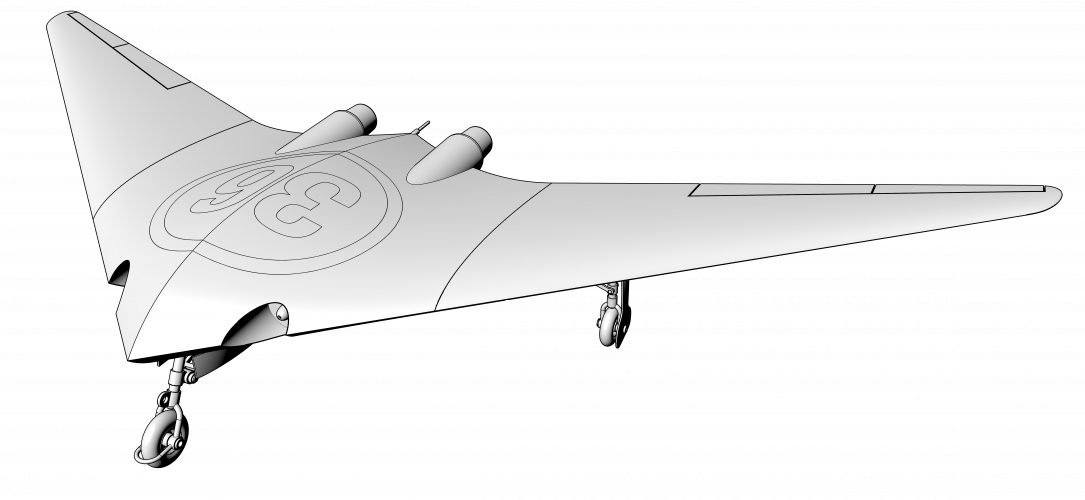
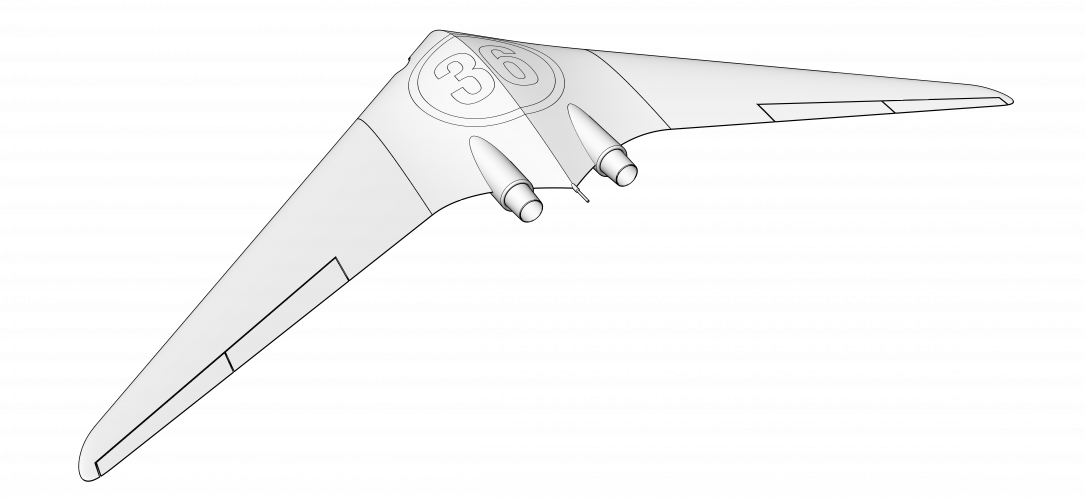
So let me introduce you a Area Rule's graphic method.
There is no double & triple integrals or some complex mathematics with no shape representation in the end.
Any comments welcome
Hello and thanks for you kindness!Welcome to the forum!
Nice drawing! However, what is the method? Can you elaborate?
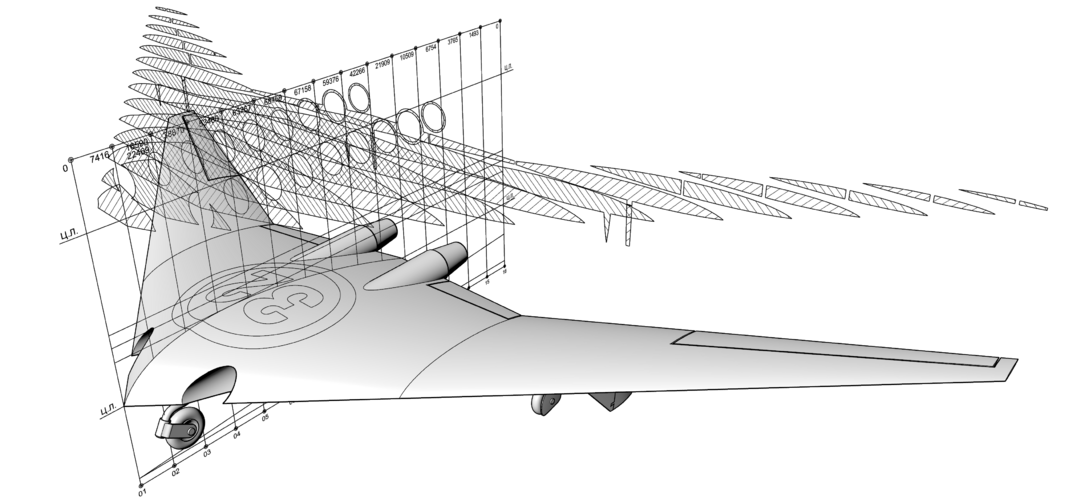
Hello and thanks for reply, to be honest I thought the sameYou might change the vertical grid to red or green to separate it from the background.
Hello gwiz,Takes me back to the start of my career. We had a little program to get the wave drag from the area distribution, but the drawings were still done by hand and I spent a lot of time with a planimeter actually getting those area distributions to input. Things soon got easier when the wing geometry was digital and I only had to measure the fuselage, but it was quite a time before the whole aircraft was digital.
Question for you, since I don't have enough of an engineering background to understand much of the area rule other than "it's needed."Takes me back to the start of my career. We had a little program to get the wave drag from the area distribution, but the drawings were still done by hand and I spent a lot of time with a planimeter actually getting those area distributions to input. Things soon got easier when the wing geometry was digital and I only had to measure the fuselage, but it was quite a time before the whole aircraft was digital.
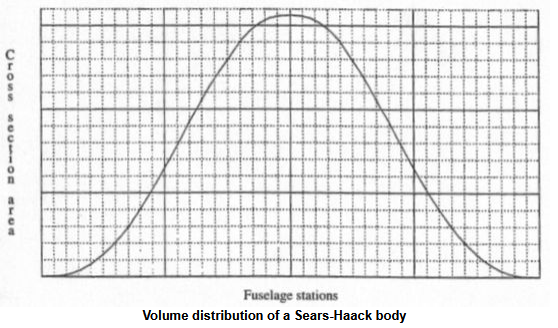
It's not sounding like that's what I meant.Yes, look up Sears-Haack body.
The method was applied to the cross-sectional area distribution using cutting planes tangential to the Mach cone and averaged over roll angle around the cone. If there was a difference between area at the nose and tail, eg a blunt base like a rocket, the Von Karman ogive between nose and tail was subtracted leaving a distribution pointed at both ends. The optimum shape for the residual area distribution was the Sears-Haack one, but the actual wave drag was calculated from the formula, the double integral one, in the Wikipedia entry for Sears-Haack. As the formula uses the second derivative of the area distribution, it is highly sensitive to the smoothness of the distribution.@[user-BG]'s method puts the area change into a nice smooth curve if the area ruling is done correctly. Is there some optimum shape to this curve that you can express as a math formula? (basically working backwards from this formula to make the plane shape)
Ugh. Way over my math paygrade (I didn't do so well in Calculus, though I didn't find it all that hard. Just didn't do anywhere near enough problems to internalize the formulas.)The method was applied to the cross-sectional area distribution using cutting planes tangential to the Mach cone and averaged over roll angle around the cone. If there was a difference between area at the nose and tail, eg a blunt base like a rocket, the Von Karman ogive between nose and tail was subtracted leaving a distribution pointed at both ends. The optimum shape for the residual area distribution was the Sears-Haack one, but the actual wave drag was calculated from the formula, the double integral one, in the Wikipedia entry for Sears-Haack. As the formula uses the second derivative of the area distribution, it is highly sensitive to the smoothness of the distribution.
Bugger.In the transonic region, the equations describing the flow are a lot more complicated than in pure subsonic or supersonic flow and you need a full CFD method to get good predictions.
Second this!Can you import an F102 and then an F106 to highlight the effect on essentially the same design
Hello and thanks for the interest on my topic.Question for you, since I don't have enough of an engineering background to understand much of the area rule other than "it's needed."
@[user-BG]'s method puts the area change into a nice smooth curve if the area ruling is done correctly. Is there some optimum shape to this curve that you can express as a math formula? (basically working backwards from this formula to make the plane shape)
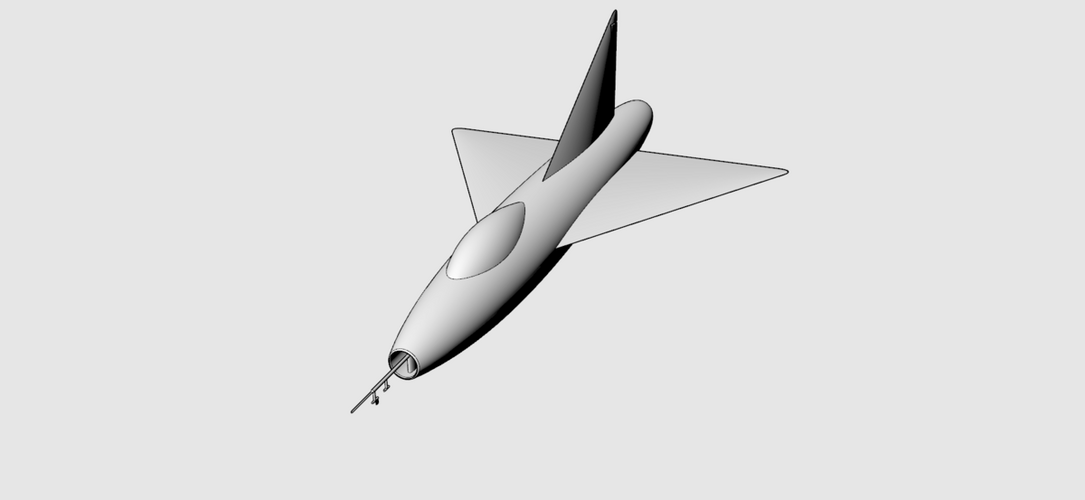
Hello, thanks for reply.Can you import an F102 and then an F106 to highlight the effect on essentially the same design
Hello, thanks for reply.
Please pay attention to the tubes of both planes - sections where wings are decreased just because of Area Rule.
However, I think a lot of things can be improved in those planes also on a lot of existing planes build in hundreds.
Regards
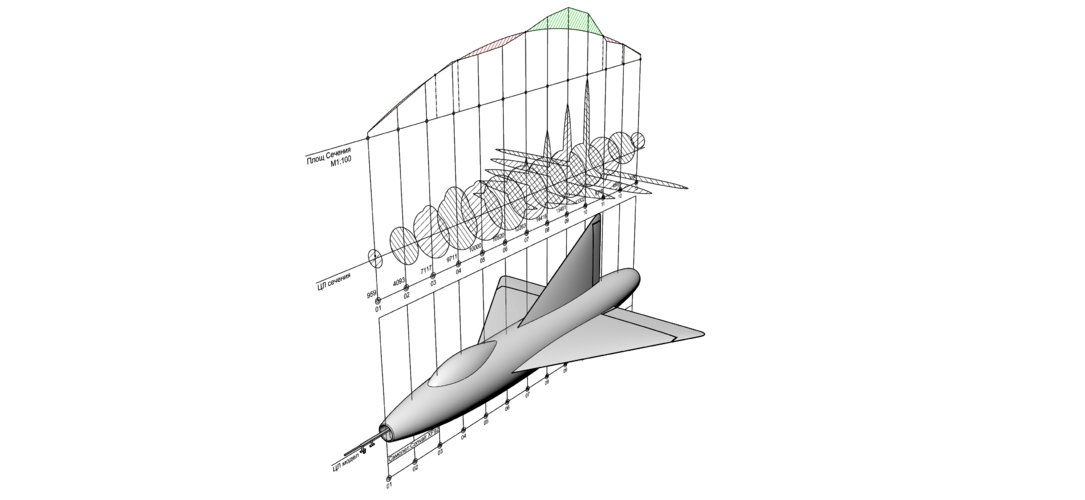
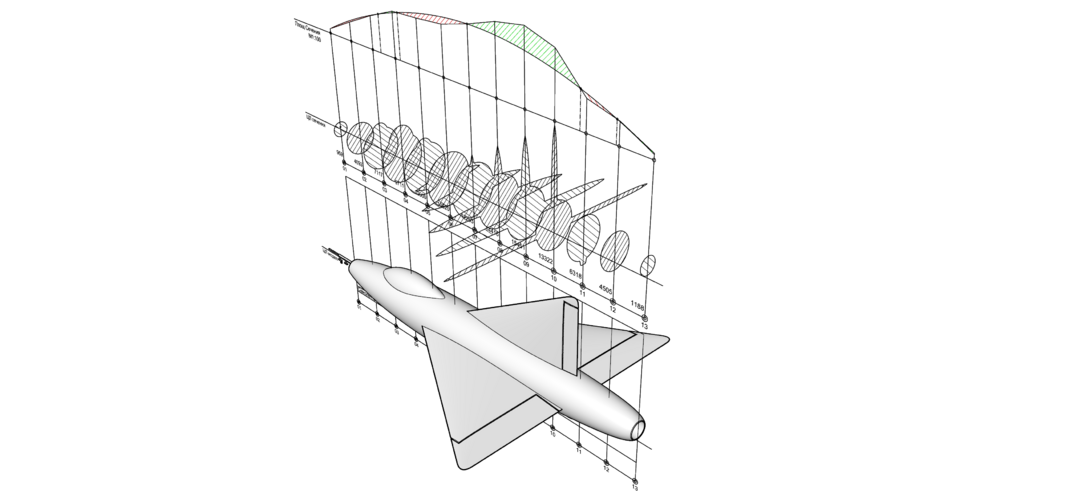


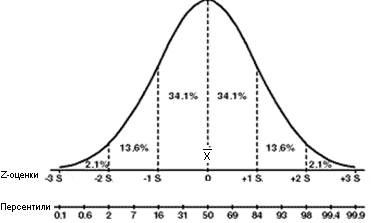
Hello richiebogie,Hi. You mention that the normal distribution is the optimal curve for the area rule.
However this article says the semicircle is optimal:

The Transonic Area Rule
In the early 1950s, a few years after Chuck Yeager broke the ‘Sound Barrier’ using the rocket powered Bell X-1, American aerospace…teamarcis.medium.com
It looks like a bit less than a half circle.
If you want to keep the second derivative low, then it would make more sense to use a quarter circle and start with the gradient of the surface area curve at 1 and ending at -1.
Another alternative could be a half sine curve from 0 to pi/2.
Eg. For an airplane of length L, the cross-sectional area would follow f(x) = sin(pi*x/2L) for x = 0 to L
Or it could be a full sine curve from -pi/2 to 3*pi/2.
Eg. For an airplane of length L, the cross-sectional area would follow f(x) = 1/2sin(2pi*x/L-pi/2) +1/2 for x = 0 to L
Most of these options suggest a short and stumpy plane is optimal, a bit like an NFL football.
Where did you get the idea for a normal distribution? Was this from a journal?
It would be interesting to see how each of these options changes your designs!