Supersonic STOVL

[PMN1]

There have been supersonic STOVL designs prior to the F35B, how did their projected speed, range, payload etc compare to that expected for the F35B?

If there had been an earlier commitment, how much sooner could an aircraft with the F35B’s expected performance (though not necessarily its stealthyness) have been developed?

 

[Mike Pryce]

I think the P.1154 of 1965 was a real possibility (I know, PCB was a problem etc., but a resolveable one IMHO). AFAIK, speed, range etc. were similar to the STOVL JSF, but of course such comparisons cannot fairly be made.

 

[CammNut]

The EWR VJ-101C did VTOL and went supersonic - but never on the same flight, so no "Mission-X" - does that count? Still pretty impressive for the early 1960s, even if it did chew holes in the concrete.

http://www.tomtom-net.de/resources/vj101/vj101.htm

 

[Archibald]

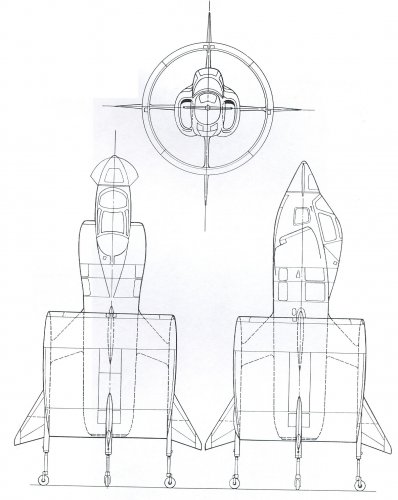
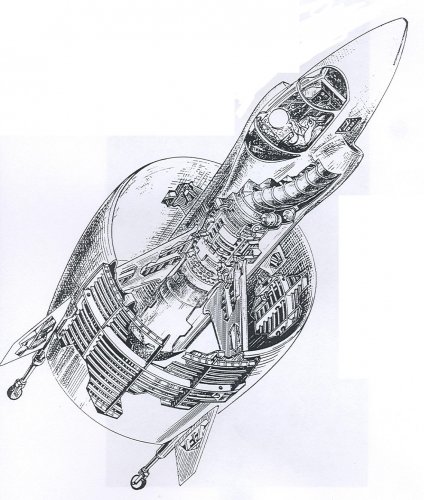
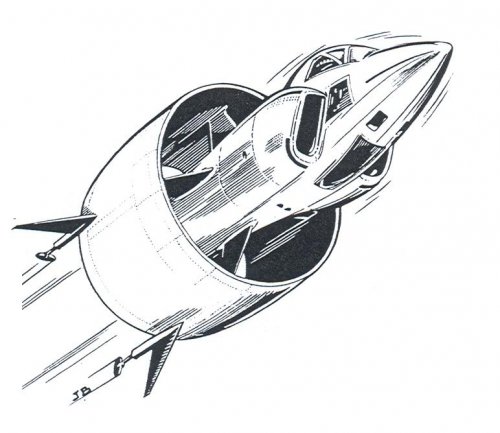
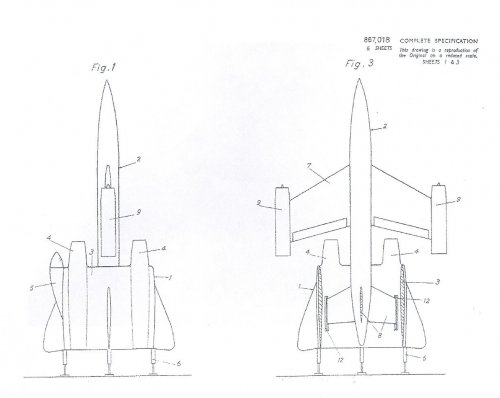
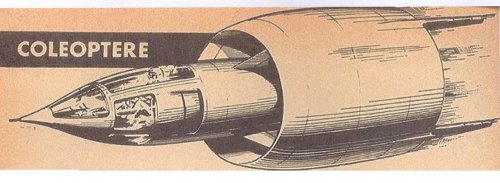
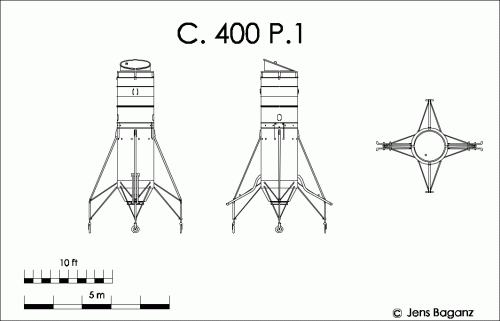
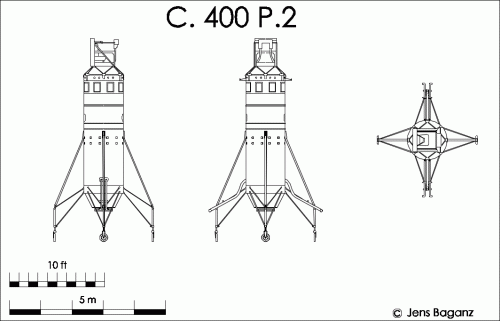
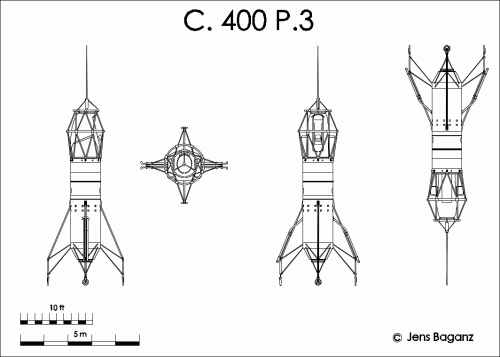
Viable supersonic V/STOL before the F-35 ? short list

- General Dynamics 200 (a kind of american Yak-41, competitor to the XFV-12 circa 1974)
- Yak-41 freestyle
- Hawker P.1216 (PCB)
That's all!

Let's see... five countries atempted to make supersonic V/STOL fighters. 2 countries produced non-viable designs, and never tried again ;D
3 others founds better solutions, but politics delayed or cancelled programs various times...

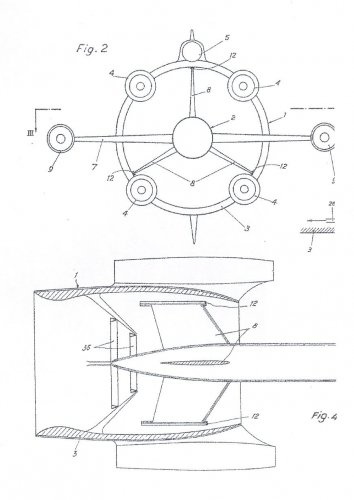
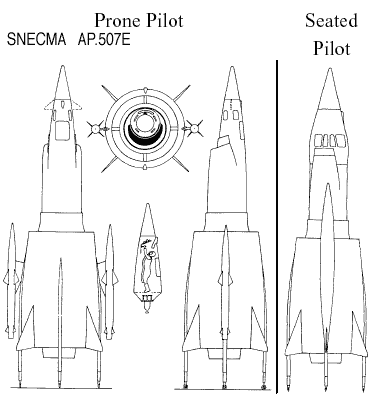
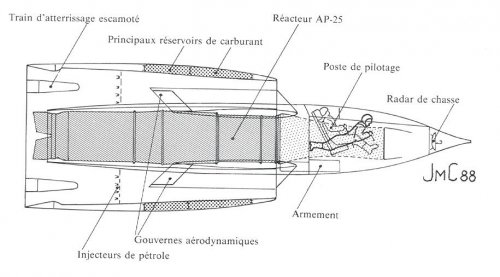
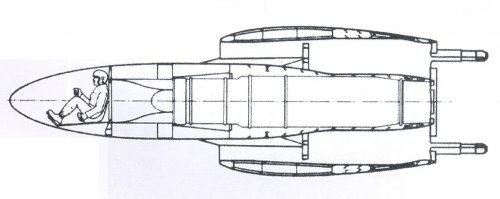
France
Mirage IIIV = eight lift jets. Evolved variants with RB-189 would have been better, but the whole concept is flawed from the start. Game over!

Germany
VJ-101C = non viable, too.

What sounds very, very odd is the fact that both VJ-101 and Mirage IIIV were the best performing V/STOL of the 60's
(VJ-101 = first to reach mach 1,
Mirage IIIV = first to reach mach 2!)
but paradoxically they were the less viable!

GB, USA and USSR obtained much better results.

Great britain pushed the Harrier excellent propulsion system to its limits (PCB, RALS) but politics, lack of funds and interest prevented any Harrier successor to be built. :'(

USSR
They found a good layout (tilting exhaust+ two lift jets) but end of Cold War prevented Yak-41 to enter service

USA
They tried a whole bunch of solutions, none worked, an opportunity was missed with the SCS fighter program in the 70's (the Rockwell XFV-12 never worked).

And now, let's see how the F-35B will work...

 

[PMN1]

STOVL EFA

In his book 'British Secret Projects, Fighters since 1950', Tony Buttler says 'A long debate during Eurofighter's development concerned whether it should be designs for STOL or STOVL'

What impacts would a STOVL decision have had - presumably the UK does not get involved in JSF??

 

[Mike Pryce]

What impacts would a STOVL decision have had....?

This:

http://www.secretprojects.co.uk/forum/index.php/topic,308.0.html !

 

[Mike Pryce]

See also this thread:

http://www.whatifmodelers.com/forum//index.php?showtopic=16192&hl=p116&st=0

which has pics of the similar P.116

 

[PMN1]

Could the various engine designs developed for the JSF have been used on earleir designs?

 

[Archibald]

Hmmm IHMO Overscan, I think its time to merge some threads on V/STOL fighters...

 

[PMN1]

How would the BAe P.1216 have compared to the expectations for F35B in terms of weapons load and range?

 

[sferrin]

Could the various engine designs developed for the JSF have been used on earleir designs?

How? The engines even NOW are still in developement, how could they have used them in earlier designs?

 

[PMN1]

Could the various engine designs developed for the JSF have been used on earleir designs?

How? The engines even NOW are still in developement, how could they have used them in earlier designs?

No, what I am saying is, could the arrangement being used now in the F35B have been developed sooner if that arrangement been picked or is it only now the required engine efficiencies make it possible?

 

[sferrin]

Could the various engine designs developed for the JSF have been used on earleir designs?

How? The engines even NOW are still in developement, how could they have used them in earlier designs?

No, what I am saying is, could the arrangement being used now in the F35B have been developed sooner if that arrangement been picked or is it only now the required engine efficiencies make it possible?

Oh. From what I understand that shaft driven lift fan is pushing even today's limits in materials because of the strength/weight requirements. Plus look at the power of the engine needed to drive that sucker.

 

[Michel Van]

you forgot a French project

SNECMA C450 coléoptère
a ring wing Tail-sitter with a ATAR E-5-V Jet-engine

the Program was only financed by SNECMA
they lost the only prototype after first transition from vertical take-off to aerodynamic flight back
the problem was: the Testpilot had not enough practise flight with C450
More here http://jpcolliat.free.fr/xfv1/xfv1-8.htm
(use flags for translate the french text)
C450 was only technical demonstrator for SNECMA AP.507E a Mach 3 Ringwing VTOL jet/Ramjet Fighter

 

[Justo Miranda]

Here some additional stuff of SNECMA C.450 and test rig (post 1)

 

[Justo Miranda]

Here some additional stuff of SNECMA C.450 and test rig (post 2)

 

[Justo Miranda]

And the supersonic version ...

 

[Michel Van]

SNECMA AP.507E a Mach 3 Ringwing VTOL jet/Ramjet Fighter

 

[Justo Miranda]

I love tailsitters...

 

[Jemiba]

Three successive versions of the "flying ATAR" :

 

[sferrin]

Look more like lunar landers ;D

 

[Jemiba]

"Look more like lunar landers"

... and probably similar in handling !

But I think, one of those "flying ATAR" was later fitted with a mock-up
nose of the C.450, too, the test rig seems not to have a jet engine.