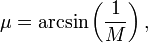KJ_Lesnick said:
...
Let's hope I don't get a heart-attack
Hey KJ.
Let's learn a relatively simple way of calculating this.
Many years ago I posted a simple calculation on how to compute this on the skunk-works
mail list.
The technique uses the CIT (Compressor Inlet Temperature) max for the J58 and looks
up important parameters from the SR-71 dash-1 flight manual.
Per the SR-71 Dash-1 flight manual, pg. 1-18, "Compressor Inlet Temperature (CIT) Gage",
"A dial indicating CIT gage is mounted on the left side of the pilot's instrument panel.
L (left) and R (right) needles indicate the total (ram) air temperature forward of the first
compressor stage in the corresponding engine inlet. ..."
The key word here is "total (ram) air temperature". This means something very specific to
an AE enthusiast. If you look in a basic aero textbook, this is a reference to:
"total temperature" for which there is a very simple algebraic equation:
T0/T = 1 + ((lambda - 1)/2) * M**2.
T0 is the total temperature, or the temperature the air would be at if it was isentropically (ie:
without losses, or modelling a perfect inlet) brought to rest from its freestream speed, or
maximum mach number of the SR-71.
T is the ambient temperature at the flight altitude (say 85,000 ft).
lambda is the ratio of specific heats, or 1.4. As far as we're concerned, a constant.
M is the Mach number.
So why is this important?
Because Bill Brown the head of the Pratt&Whitney J58 program has been quoted in a number of
publications (ex: Lockheed Horizons Winter 1981/82), that CIT design was for 800 deg F (427 deg C
or 700 deg K).
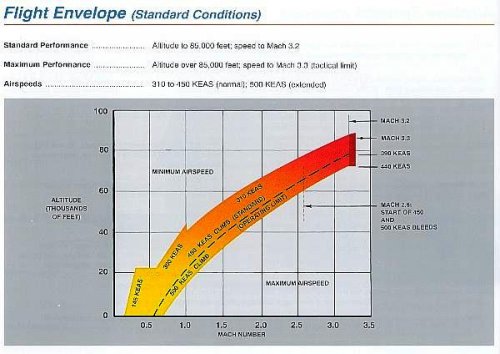
Also, the SR-71 dash-1 flight manual on pg 1-20, Fig 1-11, "Compressor Bleed and IGV Shift Schedule"
on the bottom axis, which is both in Mach Number and CIT deg C, the CIT scale goes up to
400 deg C, again agreeing with what Bill Brown said in Lockheed Horizons (above).
So let's use the simple formula I mentioned, to calculate the Mach number
corresponding to CIT max (427 deg C, 700 deg K, or 800 deg F), at 85,000 ft, with lambda at 1.4.
The original equation (above) can be rearranged to solve for Mach No as follows:
((T0/T) - 1) / ((lambda - 1)/2) = M**2
Now just plug in the numbers:
T0 = 700 deg K (CIT max per Bill Brown and the SR-71 dash-1 Fig 1-11)
T = 219 deg K (ambient temp at roughly 85,000 ft - look this up in an aero engineering book)
Lambda = 1.4
We will solve for Mach number given these input parameters, as follows:
((700/219) - 1) / ((1.4 - 1)/2) = M**2
(3.196 - 1) / (.4/2) = M**2
2.196 / .2 = M**2
10.98 = M**2
3.31 = M
There you have it !!
Max mach number of 3.31 at 85K ft. corresponding to a CIT max of 427 deg C
per the SR-71 dash-1 flight manual. By the way, this completely agrees with
the Mach number scale at the bottom of Fig 1-11 in the SR-71 Dash-1 as
well, but instead of reading it off the axis we calculated it.
It's just AMAZING what you can do with simple aero engineering equations.
This stuff is POWERFUL !!
Now another tidbit, again showing the power of physics as embodied in aero
equations and math and what you can do with it.
I nopticed that according to the SR-71 dash-1 flight manual, that the CIT gage
has a max reading. That max reading is 500 deg C (932 deg F, 773 deg K).
Your homework is to calculate the Mach number corresponding to that at
85,000 ft using lambda at 1.4 again.
No I'm not saying the SR-71 would do that. We have simply noticed that the
CIT gages in the cockpit go up to 500 deg C and we are merely using these
powerful AE equations to observe some things !!
Enjoy!!