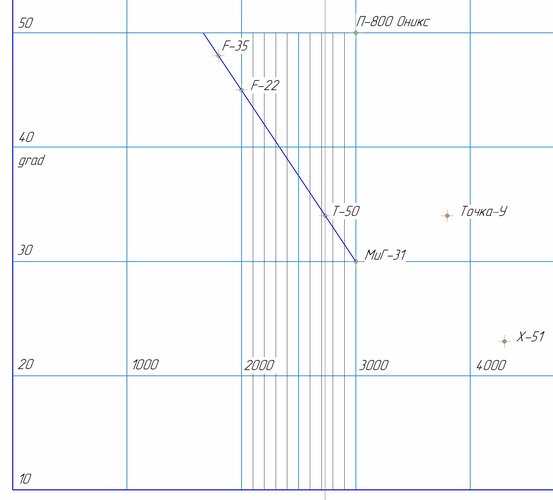
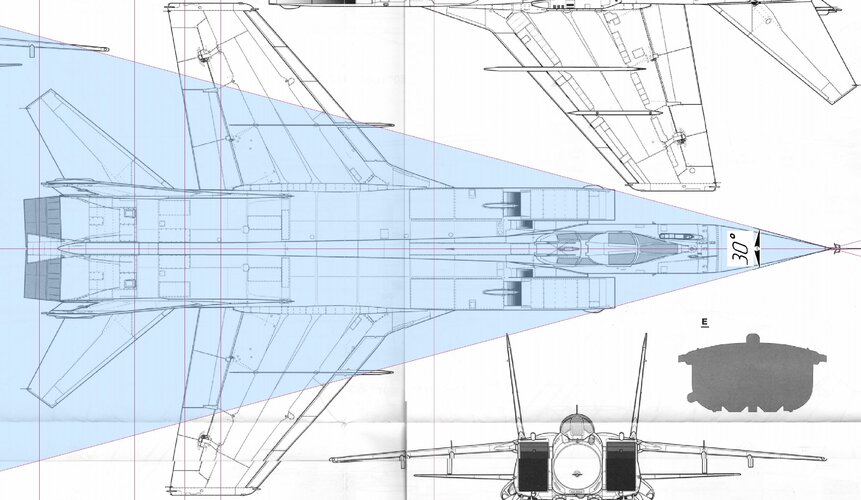
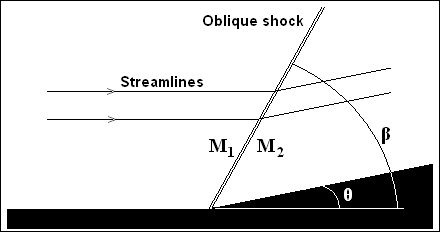
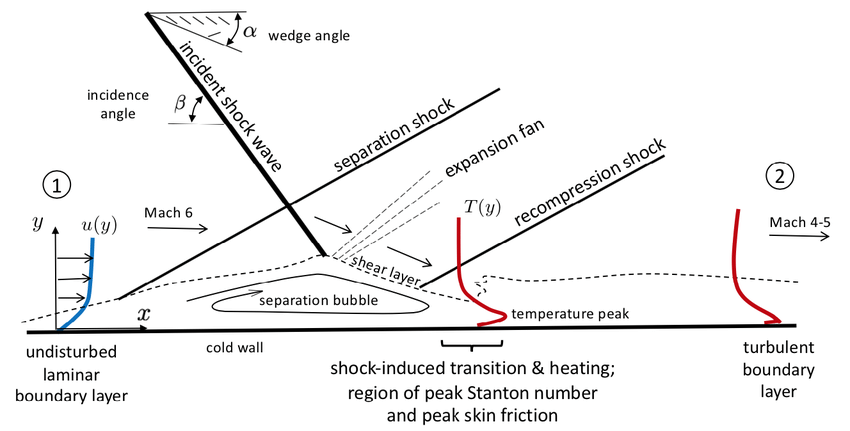
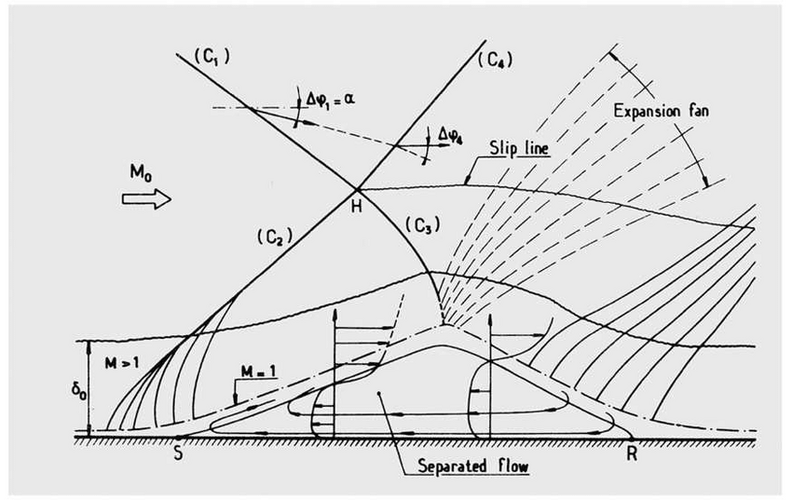
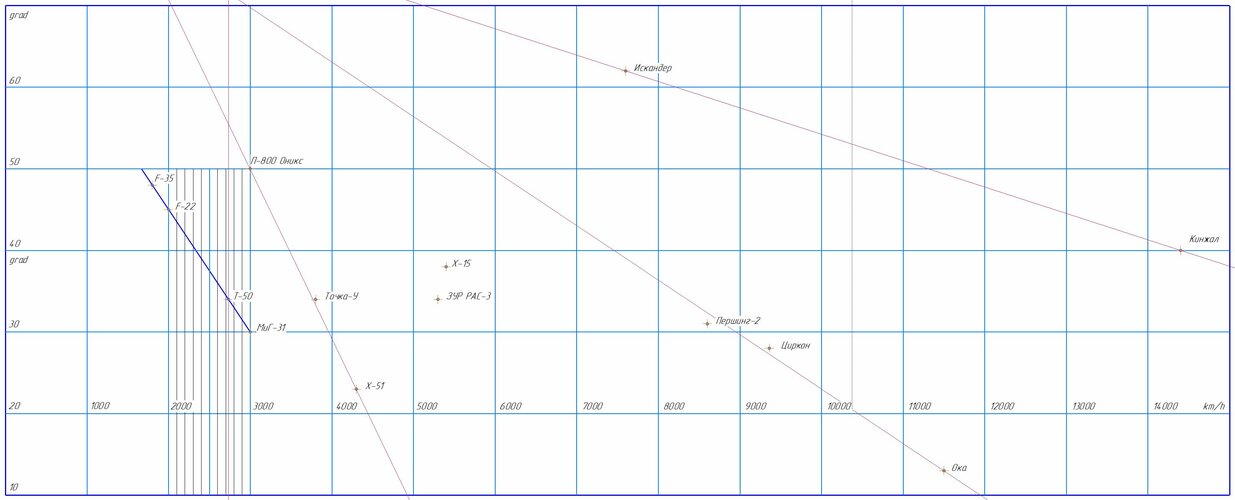
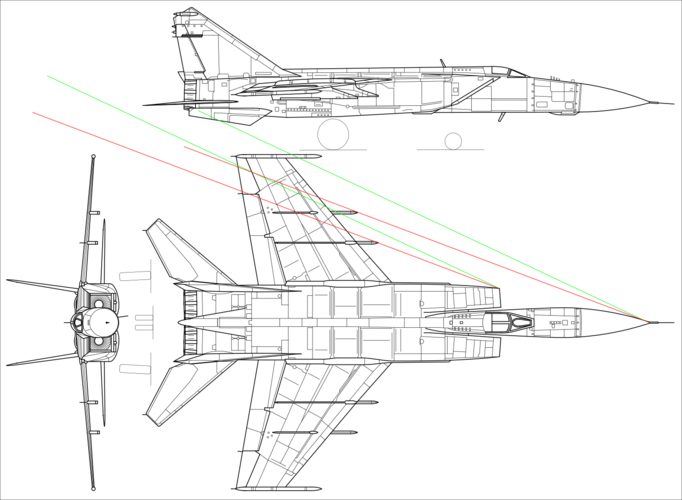
In aircraft, the sweep of the leading edge of the wing is directly related to the estimated flight speed. There are exceptions to the rules, but there are not many of them
F-22 - 42 grad
Su-57 - 48 grad
(48 : 42) * 1593 km/h = 1820 km/h
F-22 - 42 grad
Su-57 - 48 grad
(48 : 42) * 1593 km/h = 1820 km/h
Last edited: