SNCASO (Sud-Ouest) SO.8000 « Narval »

[hesham]

Hi,

do anyone have a drawing to SNCASO-8010 which fitted with Rolls-Royce Nene
turbojet engine.

 

[Jemiba]

HANDLE WITH CARE !
It's just a try of a visualisation, done with the help of the description
and comparison with similar types, like the Saab J21.

But as someone mentioned a monography about the SO Narval, I'm
still hoping for a better source ! ;D

 

[Barrington Bond]

The Aeroplane 6 May 1949.

Carrier borne fighter, twin booms, Jumo 213 engine contraprop.

 

[blackkite]

This beautiful aircraft was also unique,too.

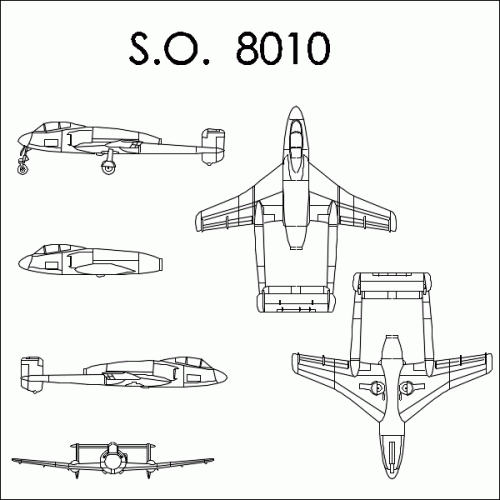
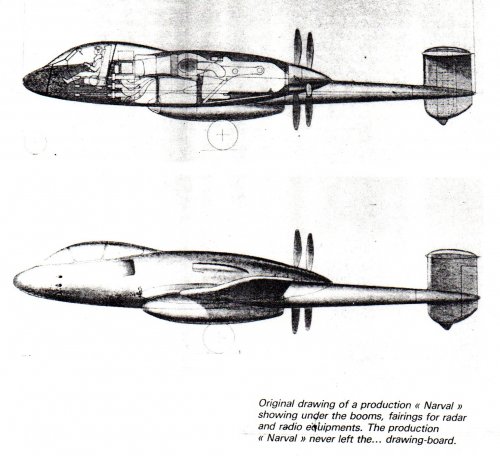
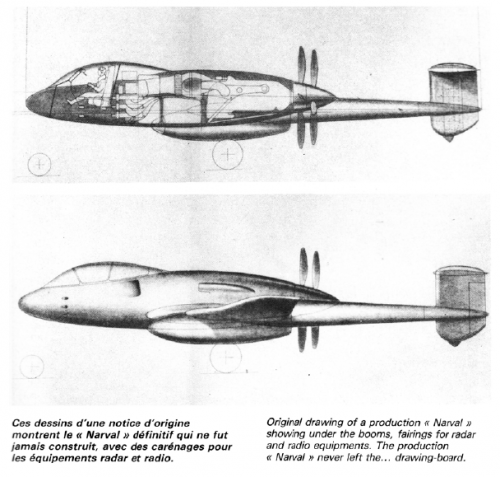
"The pilot was enclosed in a sliding bubble-style canopy near the front of the aircraft. This configuration provided the pilot with an excellent view. Behind the cockpit and on each side of the aircraft were cooling air intakes for the radiator. After flowing through the radiator, the cooling air exited around the spinner of the eight-blade contra-rotating propellers. The air intake for the Arsenal 12H engine was located on the upper left side of the rear fuselage."

https://oldmachinepress.wordpress.com/2014/01/25/sud-ouest-sncaso-so-8000-narval/

 

[Stargazer2006]

A favorite of mine among French prototypes.

May I suggest renaming the topic as "Sud-Ouest S.O. 8000 Narval" for easier reference? Thanks.

 

[blackkite]

Hi!
https://www.youtube.com/watch?v=mqc0ZHQP4As

https://www.youtube.com/watch?v=uk3Gqig2WSo

 

[XP67_Moonbat]

Thought this was postwar? Mods, maybe we could merge this with that existing thread.

 

[Michel Van]

Thought this was postwar? Mods, maybe we could merge this with that existing thread.

yes this was late 1940s, prototype fly in 1949
in 1950 the project was stop for two reasons, Aircraft needed more powerful engine and French Navy wanted jet engine aircraft

 

[blackkite]

Oh sorry. It was a postwar project?
French engineer wanted to develop ultimate liquid cooling engine fighter.

Jumo213 engine. "pressurized cooling system"
https://en.wikipedia.org/wiki/Junkers_Jumo_213

 

[Zizi6785]

One more picture:

 

[blackkite]

Beauty. Almost jet fighter. Wing shape is impressive. Why such a complicated wing shape?

 

[Stargazer2006]

Beauty. Almost jet fighter. Wing shape is impressive. Why such a complicated wing shape?

Because we French people believe in this saying: "Why make things simple when they can be complicated?"

Just kidding. Except for paperwork and administration of course, where unnecessary complication seems to be the rule.

 

[galgot]

Beauty. Almost jet fighter. Wing shape is impressive. Why such a complicated wing shape?

I suppose they did that all trailing edge flaps system to have low speed when landing on a carrier.
But wonder were they would have placed the arresting hook ?...
Indeed nice shape.

 

[Justo Miranda]

Some info-1

 

[Justo Miranda]

Some info-2

 

[Justo Miranda]

Some info-3

 

[Justo Miranda]

Some info-4

 

[Justo Miranda]

German version

 

[Justo Miranda]

Beauty. Almost jet fighter. Wing shape is impressive. Why such a complicated wing shape?

I suppose they did that all trailing edge flaps system to have low speed when landing on a carrier.
But wonder were they would have placed the arresting hook ?...
Indeed nice shape.

D.H. Venom solution?

 

[galgot]

But the prop would have been there...
Thanks for the images.

 

[Justo Miranda]

Solution for jet version only

 

[Stargazer2006]

Brilliant set of pics, thanks Justo!

 

[blackkite]

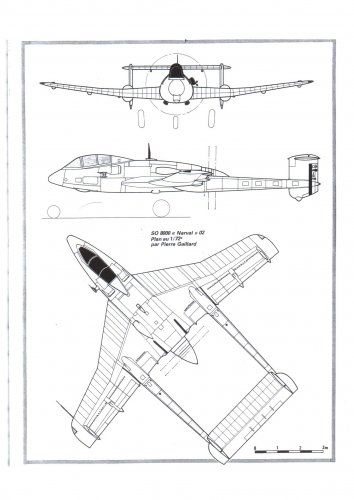
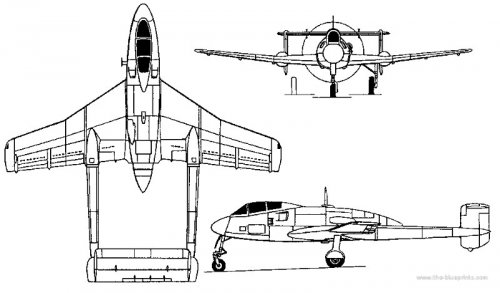
Many thanks justo for excellent and surprising 3-side view and general arrangement for production model.
We can see radiator, cooling fan and relation between ram air intake and engine.
We also see radar under the boom.

 

[blackkite]

Hi! Some information.
http://www.whatifmodelers.com/index.php?topic=4626.75;wap2

"- in 1948 was designed the improved SO.8010 jet (3-view in the same Docavia book). None ordered. THE END..."

What is Docavia book??

 

[Jemiba]

Docavia is a series of books from the French publisher Editions Larivière (https://fr.wikipedia.org/wiki/Collection_Docavia ),
containing amongst otheres the volumes "Les Avions De Combat Francais", "Les Avions Breguet", "Latécoère,
les avions et hydravions" or "René Leduc. Un pionnier de la propulsion à réaction", all credited as sources in
several threads here and all containing dozens of projects.
Nevertheless, if there really is 3-view of the SO.8010, I'm not sure. The SO.8000 is shown without doubt, but
IIRC the 8010 is described in the text only.

 

[blackkite]

Hmmm....Anyway thanks a lot.
This book?

 

[Justo Miranda]

Pure gold

 

[Justo Miranda]

French available info

 

[Stargazer2006]

Pure gold

Absolutely. For many years (1970s through 1990s) Editions Larivière set a standard for quality, both in their monthly publication Le Fana de l'Aviation and their authoritative (and often definitive) Docavia books that is sadly missing today, as none of their recent releases quite matches them.

Docavias on French aircraft are of course amazing, but volumes such as the ones on Grumman or Vought, for instance, are still unmatched in any language to this day.

 

[blackkite]

We strongly need after 1960 volume. Hip,Hip Hooray French.

 

[hesham]

From Le Fana 180;

 

[acegeek9992]

We strongly need after 1960 volume. Hip,Hip Hooray French.

Which planes are depicted in that pic? I think I recognize the Super Vautour, but the rest I have zero clue about

 

[hesham]

Which planes are depicted in that pic? I think I recognize the Super Vautour, but the rest I have zero clue about

You can find them here;

https://www.secretprojects.co.uk/threads/dassault-mach-3-mirage-fighter-projects.12481/