Piaggio 133 was like b-24

[airman]

scanned for you from "Aerei nella Storia" of this month !
Simply design of Piaggio 133 was strictly connected to B-24 !

 

[lark]

Great! Thanks a lot.

 

[Skybolt]

I beg to differ... captured B-24 data and drawings were disseminated in all the Italian companies by the DSSE in Guidonia. There is a copy of the very same document in the SIAI-Marchetti archive (along with an analysis of the Lightning ... ). There was interest in the B-24 wing, engines and instrumentation, but to postulate a deriivation is ridicolous, just look at the plans... (the wing is totally different) I think the all thing is a typical "name setting" stunt.. since the P.108 is "The Italian Flying Fortress" (false, just look at the defensive armament), it is nice to define the P.133 like "the Italian Liberator"... Now I'll post the P.130 high-altitude bomber project and define it the "Italian Superfortress"...

 

[lark]

In the side view the Piaggio 133 looses indeed already it's resemblence with the B-24...

Interestingly ,a Piaggio P 108bis is shown.Was this a development of of the P 108
or a side development ?

 

[Skybolt]

Hi Paul ! The 108bis was simply an early designation of the P.133, originally assigned to the sixth production series of the P.108B.

 

[lark]

Aha, now I understand!

Thanks Sky.

 

[Nico]

Hi Skyman, Lark, Skybolt and other friends,
delving in my ever out of order archives, I met the picture I think is the only known hardware really built of the Italian P.133 long range bomber.
Answering previous posts, evidently the headline of the article for "Aerei nella Storia" was an exaggeration: as Skybolt already said, headline makers (but also the model kit marketing directors) are looking for some effect in naming their subjects.
Notwhitstanding that, I had the occasion of have a look at the archives of Eng. Giovanni P. Casiraghi, technical director of Piaggio, and I saw he had a special file for pictures and documents about some aircraft of special interest. I saw a lot of photographs of the B-24, of the North American/Ryan Navion (of interest for the development of the P.149), of the Martin Mariner (in the same class of the P.155), of the AeroCommander (for the development of the P.166) etc.
Sure, the B-24 and the P.133 are quite different projects, but indeed for Regia Aeronautica the P.133, if built, would be something in the same ballpark of Liberator...
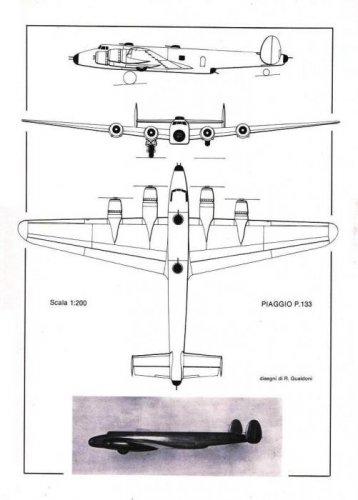
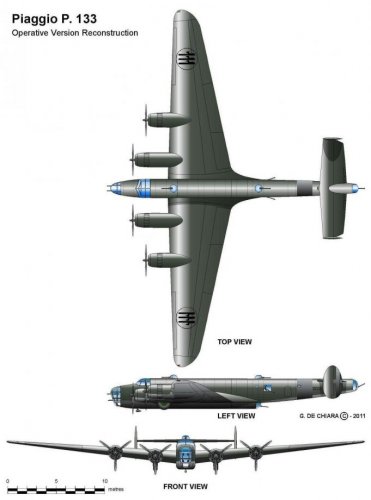
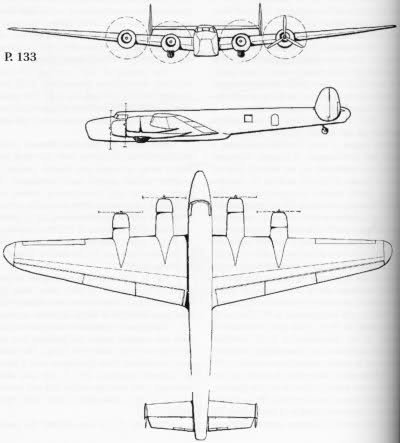
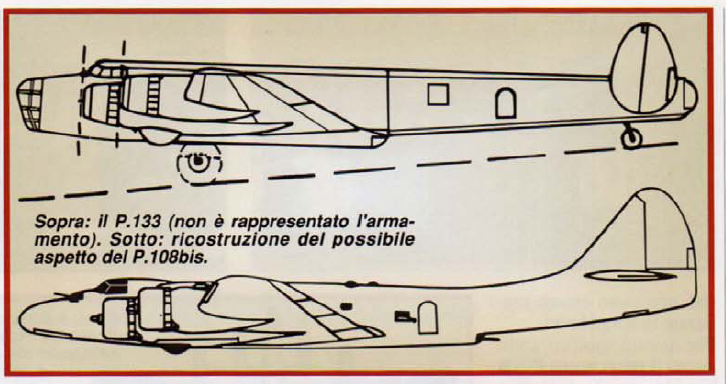
In fact, we have very scant information about the P.133 and is a matter of fact that during its development it was completely redesigned (apart for planform) in respect to P.108B and the early P.108bis concept.
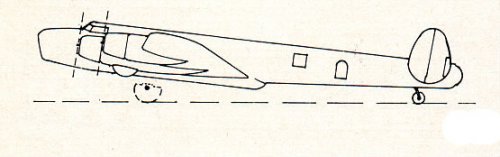
We lack any accurate three-view drawing and also the artist's impression that appeared on the feature of "Aerei nella Storia" was largely an interpretation of the illustrator. Anyway, I still think the development of P.133 was at some extent influenced by other bombers of the time, as the Liberator and the Lancaster. As you can see in the enclosed drawing by late Giorgio Bignozzi, the section of the P.108B fuselage was circular from the wing trailing edge to the extreme tail and the fin and rudder was single. The wind tunnel model of P.133 sports a rectangular fuselage and twin fin and rudders (like the Liberator) and a nose very similar to the one of B-24D.
The enclosed picture of the fuselage section that appears on the book of Giancarlo Garello ("Il Piaggio P.108"), captioned as a section of the fuselage construction of P.108B, has flat sides and seems to be consistent with one of the first structural parts (perhaps the only) really built of the P.133 prototipe (serial number MM.26248) ordered when the project was cancelled by the German authorities, after the September 8, 1943, armistice.
Thank you for your interest in Italian projects
Nico

 

[hesham]

... Now I'll post the P.130 high-altitude bomber project and define it the "Italian Superfortress"...

My dear skybolt;

you sent it before;

http://www.secretprojects.co.uk/forum/index.php/topic,623.0/highlight,piaggio+p+130.html

 

[Skybolt]

Thanks Nico ! According to Giancarlo's book (BTW, I met him yesterday at lunch with a bunch of other aerofriends: Giovanni Massimello, Paolo Valdis, Enrico Leproni, Giorgio Apostolo, Maurizio Pagliano, Gianni Cattaneo, it was FUN) the prototype of the P.133 was completed in Finale up to the crossing of the fuselage with the wings, and after Setp. 8 1943 was initially hidden in the Ghigliazza cave and then demolished.
As for the photo, it could be what you say, but the area where the wings attach to the fuselage (the indent on the right in the fuselage structure) from this angle of view seem too low for the mid, fuselage passing wings that the P.133 is known to have had. I could be wrong, but it looks like a normal low-wing P.108 structure (could be a "T", just look at the photo published by Giancarlo at page 35 of his book). Unfortunately, the tail area isn't visible, and THAT would have been decisive.

 

[blackkite]

Hi!
I can see two nose shape for P.133.

 

[blackkite]

Another nose shape.

http://www.secretprojects.co.uk/forum/index.php?action=dlattach;topic=5085.0;attach=125667;image

 

[zeroc]

Hi, all.
My usual two cents about Italian unbuilt aircrafts.
Happy New Year,
Marco

 

[hesham]

From, Aerei Nella Storia 61.

 

[Luftwaffe1946]

This is my piaggio p.133 scratchbuilt in 1:72

 

[Hardrada55]

Outstanding! What is the weapon it is carrying in the bomb bay?

 

[Luftwaffe1946]

1 x Liquid Oxygen Bomb project

 

[ImportantSimone5]

Hi Skyman, Lark, Skybolt and other friends,
delving in my ever out of order archives, I met the picture I think is the only known hardware really built of the Italian P.133 long range bomber.
Answering previous posts, evidently the headline of the article for "Aerei nella Storia" was an exaggeration: as Skybolt already said, headline makers (but also the model kit marketing directors) are looking for some effect in naming their subjects.
Notwhitstanding that, I had the occasion of have a look at the archives of Eng. Giovanni P. Casiraghi, technical director of Piaggio, and I saw he had a special file for pictures and documents about some aircraft of special interest. I saw a lot of photographs of the B-24, of the North American/Ryan Navion (of interest for the development of the P.149), of the Martin Mariner (in the same class of the P.155), of the AeroCommander (for the development of the P.166) etc.
Sure, the B-24 and the P.133 are quite different projects, but indeed for Regia Aeronautica the P.133, if built, would be something in the same ballpark of Liberator...
In fact, we have very scant information about the P.133 and is a matter of fact that during its development it was completely redesigned (apart for planform) in respect to P.108B and the early P.108bis concept.
We lack any accurate three-view drawing and also the artist's impression that appeared on the feature of "Aerei nella Storia" was largely an interpretation of the illustrator. Anyway, I still think the development of P.133 was at some extent influenced by other bombers of the time, as the Liberator and the Lancaster. As you can see in the enclosed drawing by late Giorgio Bignozzi, the section of the P.108B fuselage was circular from the wing trailing edge to the extreme tail and the fin and rudder was single. The wind tunnel model of P.133 sports a rectangular fuselage and twin fin and rudders (like the Liberator) and a nose very similar to the one of B-24D.
The enclosed picture of the fuselage section that appears on the book of Giancarlo Garello ("Il Piaggio P.108"), captioned as a section of the fuselage construction of P.108B, has flat sides and seems to be consistent with one of the first structural parts (perhaps the only) really built of the P.133 prototipe (serial number MM.26248) ordered when the project was cancelled by the German authorities, after the September 8, 1943, armistice.
Thank you for your interest in Italian projects
Nico

Sadly, the pic of P.133 under construction is not of a P.133, but a P.108.

PIAGGIO P

This is the original pic.